题目内容
已知f(x)=ax2+bx+1.(1)若f(x)>0的解集是(-1,2),求实数a,b的值.
(2)若A={x|f(x)>0},且-1∈A,2∈A,求3a-b的取值范围.
分析:(1)由一元二次不等式的解集与一元二次方程的根的关系可以得出,ax2+bx+1=0的解为-1,2,由根系关系即可求得实数a,b的值
(2)要题意可得出一关于实数a,b的不等式组,要求3a-b的取值范围可用线性规划的知识来求,以所得不等式组作为约束条件,以3a-b作为目标函数即可.
(2)要题意可得出一关于实数a,b的不等式组,要求3a-b的取值范围可用线性规划的知识来求,以所得不等式组作为约束条件,以3a-b作为目标函数即可.
解答: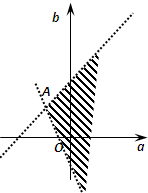 解:(1)由题意可知:a<0,且ax2+bx+1=0的解为-1,2
解:(1)由题意可知:a<0,且ax2+bx+1=0的解为-1,2
∴
解得:a=-
,b=
(2)由题意可得
,?
画出可行域,由
得{
作平行直线系z=3a-b可知z=3a-b的取值范围是(-2,+∞)
 解:(1)由题意可知:a<0,且ax2+bx+1=0的解为-1,2
解:(1)由题意可知:a<0,且ax2+bx+1=0的解为-1,2∴
|
| 1 |
| 2 |
| 1 |
| 2 |
(2)由题意可得
|
|
画出可行域,由
|
得{
|
作平行直线系z=3a-b可知z=3a-b的取值范围是(-2,+∞)
点评:本题考查一元二次不等式的应用,求解本题的关键是理解一元二次不等式的解集与一元二次方程的根的关系以及将第二问中求3a-b的取值范围的问题转化到线性规划中求解.做题时灵活转化是降低题目难度顺利解题的关键.

练习册系列答案
相关题目