题目内容
已知f(x)=ax2-blnx+2x(a>0,b>0)在区间(
,1)上不单调,则
的取值范围是( )
| 1 |
| 2 |
| 3b-2 |
| 3a+2 |
分析:求出原函数的导函数,由原函数区间(
,1)上不单调,得到关于a,b的不等式组,作出可行域,然后利用
的几何意义求其范围.
| 1 |
| 2 |
| 3b-2 |
| 3a+2 |
解答:解:由f(x)=ax2-blnx+2x,得f′(x)=2ax-
+2=
.
令g(x)=2ax2+2x-b,
因为f(x)=ax2-blnx+2x(a>0,b>0)在区间(
,1)上不单调,
所以在区间(
,1)上,存在x使得f′(x)=0,且x不是方程2ax2+2x-b=0的二重根.
即函数g(x)=2ax2+2x-b在区间(
,1)上有零点,且零点两侧的函数值异号.
又其对称轴方程为x=-
<0,则
.
其可行域如图,
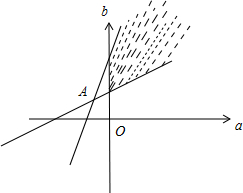
而
=
,几何意义为可行域内的动点与定点A(-
,
)连线的斜率的范围,
由图可知范围为(
,2).
故选B.
| b |
| x |
| 2ax2+2x-b |
| x |
令g(x)=2ax2+2x-b,
因为f(x)=ax2-blnx+2x(a>0,b>0)在区间(
| 1 |
| 2 |
所以在区间(
| 1 |
| 2 |
即函数g(x)=2ax2+2x-b在区间(
| 1 |
| 2 |
又其对称轴方程为x=-
| 1 |
| 2a |
|
其可行域如图,

而
| 3b-2 |
| 3a+2 |
b-
| ||
a+
|
| 2 |
| 3 |
| 2 |
| 3 |
由图可知范围为(
| 1 |
| 2 |
故选B.
点评:本题考查了函数的单调性与导数的关系,考查了简单的线性规划,考查了数形结合的解题思想方法及数学转化思想方法,解答的关键是由题意列出关于a,b的不等式组,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目