题目内容
已知f(x)=ax2+bx+c(a≠0),g(x)=f[f(x)]
①若f(x)无零点,则g(x)>0对?x∈R成立;
②若f(x)有且只有一个零点,则g(x)必有两个零点;
③若方程f(x)=0有两个不等实根,则方程g(x)=0不可能无解
其中真命题的个数是( )
①若f(x)无零点,则g(x)>0对?x∈R成立;
②若f(x)有且只有一个零点,则g(x)必有两个零点;
③若方程f(x)=0有两个不等实根,则方程g(x)=0不可能无解
其中真命题的个数是( )
分析:本题利用特殊法处理,根据已知条件,适当取特殊函数一一验证:对于①,若取a=-1,b=
,c=-
,则f(x)=-x2+
x-
,无零点;
②如下图,若f(x)(其图象为黑色)有且只有一个零点,则g(x)(其图象为红色)没有两个零点;
③如下图,若方程f(x)=0有两个不等实根(其图象为黑色),则方程g(x)=0(其图象为红色)可能无解.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②如下图,若f(x)(其图象为黑色)有且只有一个零点,则g(x)(其图象为红色)没有两个零点;
③如下图,若方程f(x)=0有两个不等实根(其图象为黑色),则方程g(x)=0(其图象为红色)可能无解.
解答: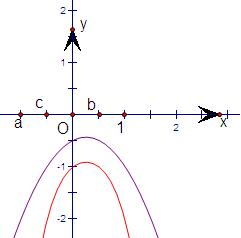 解:已知f(x)=ax2+bx+c(a≠0),g(x)=f[f(x)]
解:已知f(x)=ax2+bx+c(a≠0),g(x)=f[f(x)]
对于①,若取a=-1,b=
,c=-
,则f(x)=-x2+
x-
,无零点,如图,但g(x)<0对?x∈R成立;故①错;
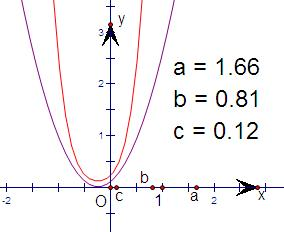
②如下图,若f(x)(其图象为黑色)有且只有一个零点,则g(x)(其图象为红色)没有两个零点;故错;
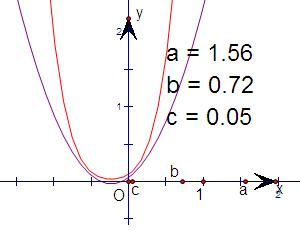
③如下图,若方程f(x)=0有两个不等实根(其图象为黑色),则方程g(x)=0(其图象为红色)可能无解,故③错.
其中真命题的个数是0.
故选A.
 解:已知f(x)=ax2+bx+c(a≠0),g(x)=f[f(x)]
解:已知f(x)=ax2+bx+c(a≠0),g(x)=f[f(x)]对于①,若取a=-1,b=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②如下图,若f(x)(其图象为黑色)有且只有一个零点,则g(x)(其图象为红色)没有两个零点;故错;
③如下图,若方程f(x)=0有两个不等实根(其图象为黑色),则方程g(x)=0(其图象为红色)可能无解,故③错.
其中真命题的个数是0.
故选A.


点评:本小题主要考查二次函数的性质、函数的零点等基础知识,考查运算求解能力,考查数形结合思想,属于基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目