题目内容
已知椭圆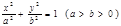 和圆
和圆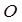 :
: ,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
,过椭圆上一点P引圆O的两条切线,切点分别为A,B. 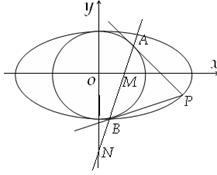
(1)(ⅰ)若圆O过椭圆的两个焦点,求椭圆的离心率e的值;
(ⅱ)若椭圆上存在点P,使得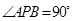 ,求椭圆离心率e的取值范围;
,求椭圆离心率e的取值范围;
(2)设直线AB与x轴、y轴分别交于点M,N,问当点P在椭圆上运动时,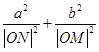 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.
(1)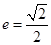 ,
,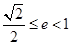
(2)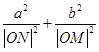 为定值,定值是
为定值,定值是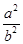 .
.
解析试题分析:解:(1)(ⅰ)∵ 圆 过椭圆的焦点,圆
过椭圆的焦点,圆 :
:  ,∴
,∴  ,
,
∴  ,
, 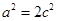 ,
,
∴ 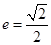 . 4分
. 4分
(ⅱ)由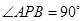 及圆的性质,可得
及圆的性质,可得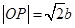 ,∴
,∴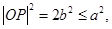
∴
∴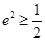 ,
, 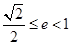 . 8分
. 8分
(2)
设 ,则
,则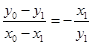 , 整理得
, 整理得
 ∴
∴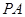 方程为:
方程为: , 10分
, 10分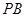 方程为:
方程为: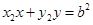 .
.
从而直线AB的方程为: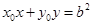 . 12分
. 12分
令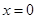 ,得
,得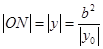 ,令
,令 ,得
,得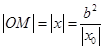 ,
,
∴ ,
,
∴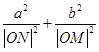 为定值,定值是
为定值,定值是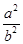 . 16
. 16
考点:直线与椭圆的位置关系
点评:主要是考查了直线与椭圆的位置关系的运用,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的角平分线, 证明直线l过定点.
的角平分线, 证明直线l过定点.  .过点P且与抛物线E交于A(xl,y1)、B( x2,y2)两点,直线
.过点P且与抛物线E交于A(xl,y1)、B( x2,y2)两点,直线 过点P且与抛物线E交于C(x3, y3)、D(x4,y4)两点.过点P作x轴的垂线,与线段AC和BD分别交于点M、N.
过点P且与抛物线E交于C(x3, y3)、D(x4,y4)两点.过点P作x轴的垂线,与线段AC和BD分别交于点M、N.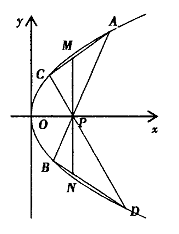
 ,一条渐近线的倾斜角为
,一条渐近线的倾斜角为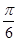 的双曲线方程。
的双曲线方程。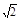 ,0),且与定圆A´:(x-
,0),且与定圆A´:(x-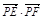 的取值范围.
的取值范围.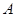 是圆
是圆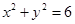 上的动点,点
上的动点,点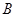 是
是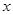 轴上投影,
轴上投影, 为
为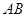 上一点,且
上一点,且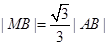 .当
.当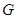 . 过点
. 过点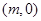
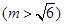 且倾斜角为
且倾斜角为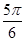 的直线
的直线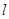 交曲线
交曲线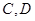 两点.
两点.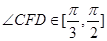 ,求
,求 的取值范围.
的取值范围.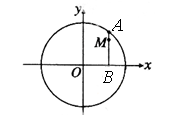
 的参数方程为
的参数方程为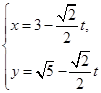 (t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为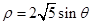 。
。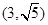 ,求|PA|+|PB|。
,求|PA|+|PB|。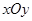 中,点
中,点 到两点
到两点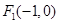 ,
,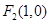 的距离之和为
的距离之和为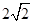 ,设点
,设点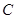 .
. (
(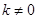 )的直线
)的直线 与曲线
与曲线 ,
, ,点
,点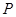 在
在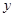 轴上,且
轴上,且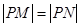 ,求点
,求点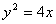 及点
及点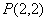 ,直线
,直线 斜率为1且不过点
斜率为1且不过点 ,与抛物线交于点A,B,
,与抛物线交于点A,B,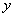 轴上截距的取值范围;
轴上截距的取值范围;