题目内容
动圆M过定点A(-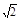 ,0),且与定圆A´:(x-
,0),且与定圆A´:(x-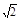 )2+y2=12相切.
)2+y2=12相切.
(1)求动圆圆心M的轨迹C的方程;
(2)过点P(0,2)的直线l与轨迹C交于不同的两点E、F,求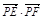 的取值范围.
的取值范围.
(1)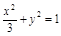
(2)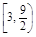
解析试题分析:解:(1)A´(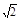 ,0),依题意有|MA´|+
,0),依题意有|MA´|+ =2
=2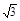 1分
1分 |MA´|+|MA|=2
|MA´|+|MA|=2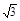 >2
>2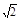 3分
3分
∴点M的轨迹是以A´、A为焦点,2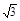 为长轴上的椭圆, 4分
为长轴上的椭圆, 4分
∵a=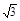 ,c=
,c=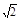 ∴b2=1. 5分
∴b2=1. 5分
因此点M的轨迹方程为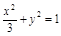 6分
6分
(2)设l的方程为x=k(y-2)代入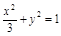 ,消去x得:
,消去x得:
(k2+3)y2-4k2y+4k2-3=0 8分
由△>0得16k4-(4k2-3)(k2+3)>0  0≤k2<1 9分
0≤k2<1 9分
设E(x1,y1),F(x2,y2),则y1+y2=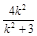 ,y1y2=
,y1y2= 10分
10分
又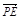 =(x1,y1-2),
=(x1,y1-2),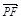 =(x2,y2-2)
=(x2,y2-2)
∴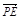 ·
·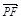 =x1x2+(y1-2)(y2-2)=k(y1-2)·k (y2-2) +(y1-2)(y2-2)=(1+k2)
=x1x2+(y1-2)(y2-2)=k(y1-2)·k (y2-2) +(y1-2)(y2-2)=(1+k2)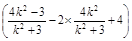 =
=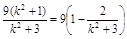 12分
12分
∵0≤k2<1 ∴3≤k2+3<4 13分
∴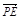 ·
·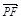 ∈
∈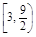 14分
14分
考点:向量的数量积以及直线与椭圆的位置关系
点评:主要是考查了椭圆方程,直线与椭圆的位置关系的运用,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
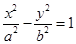 (a>0,b>0)的左、右焦点分别为
(a>0,b>0)的左、右焦点分别为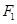 、
、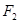 ,离心率为3,直线y=2与C的两个交点间的距离为
,离心率为3,直线y=2与C的两个交点间的距离为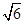 .
.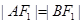 ,证明:
,证明: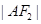 、
、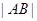 、
、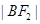 成等比数列.
成等比数列.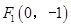 、
、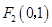 且过点
且过点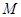
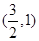 椭圆;
椭圆;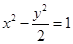 有相同的渐近线,且过点
有相同的渐近线,且过点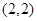 的双曲线.
的双曲线.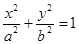 的一个焦点为
的一个焦点为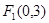 ,
,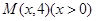 为椭圆C上一点,
为椭圆C上一点,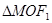 的面积为
的面积为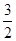 .
.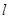 ,使得直线
,使得直线 是直线
是直线 被椭圆
被椭圆 所截得的线段中点,求直线
所截得的线段中点,求直线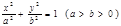 和圆
和圆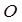 :
: ,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
,过椭圆上一点P引圆O的两条切线,切点分别为A,B. 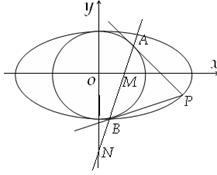
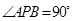 ,求椭圆离心率e的取值范围;
,求椭圆离心率e的取值范围;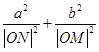 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.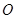 为几点,
为几点, 轴的正半轴为极轴建立极坐标系.已知直线
轴的正半轴为极轴建立极坐标系.已知直线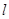 上两点
上两点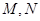 的极坐标分别为
的极坐标分别为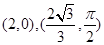 ,圆
,圆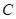 的参数方程
的参数方程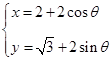 (
(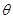 为参数).
为参数).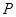 为线段
为线段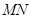 的中点,求直线
的中点,求直线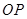 的平面直角坐标方程;
的平面直角坐标方程;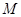 到点
到点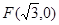 的距离与到直线
的距离与到直线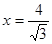 的距离之比为定值
的距离之比为定值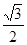 ,记
,记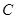 .
.
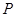 是圆
是圆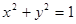 上第一象限内的任意一点,过
上第一象限内的任意一点,过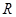 ,
,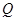 两点.
两点.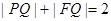 ;
;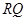 的最大值.
的最大值.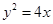 的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于
的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于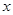 轴(垂足为T),与抛物线交于不同的两点P、Q,且
轴(垂足为T),与抛物线交于不同的两点P、Q,且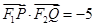 .
.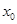 ;
;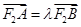 ,若
,若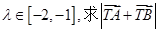 的取值范围.
的取值范围.