题目内容
设△ABC的内角A、B、C所对的边长分别为a、b、c,且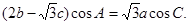
(1)求角A的大小;
(2)若角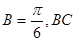 边上的中线AM的长为
边上的中线AM的长为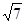 ,求△ABC的面积.
,求△ABC的面积.
(1)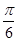 ;(2)
;(2)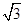 .
.
解析试题分析:(1)本题考查解三角形的知识,问题是求角,因此我们一般把已知条件中边转化为角,如果等式两边边的关系是齐次的,那么我们可以应用正弦定理转化为角,本题中已知条件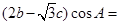
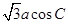 ,就可转化为
,就可转化为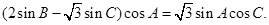 ,下面只要利用三角公式进行变形就能求出
,下面只要利用三角公式进行变形就能求出 ;(2)
;(2)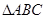 的角已经求出,但要求面积还必须至少知道两边,我们要由中线
的角已经求出,但要求面积还必须至少知道两边,我们要由中线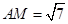 来求边,观察三角形,会发现在
来求边,观察三角形,会发现在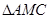 中,
中,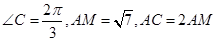 ,由此用余弦定理可求得
,由此用余弦定理可求得 的长,下面就可求面积了.
的长,下面就可求面积了.
试题解析:(1)∵ ,
,
∴ 2分
2分
即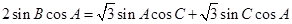 .
.
∴ 4分
4分
∵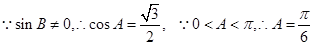 6分
6分
(2)由(1)知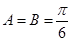 ,所以
,所以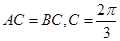 ,
,
设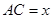 ,则
,则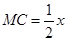 ,又
,又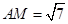 9分
9分
在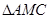 中,由余弦定理得
中,由余弦定理得
即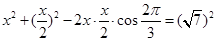 ,解得
,解得 ,
,
故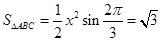 12分
12分
考点:(1)正弦定理,三角恒等式;(2)余弦定理,三角形的面积.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 中,a,b,c分别是内角A,B,C所对的边,
中,a,b,c分别是内角A,B,C所对的边,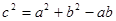 .
. 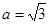 ,
,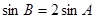 ,求
,求 中,角
中,角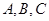 的对边分别为
的对边分别为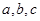 ,设S为△ABC的面积,满足4S=
,设S为△ABC的面积,满足4S=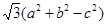 .
. 的大小;(2)若
的大小;(2)若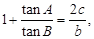 且
且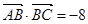 求
求 的值.
的值. ,且
,且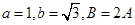 。
。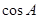 的值;(2)求c的值。
的值;(2)求c的值。 所对的边分别为
所对的边分别为 ,且
,且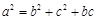 .
.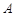 的大小;
的大小;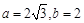 ,求边
,求边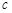 的值.
的值.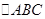 中,角
中,角 ,
, ,
,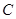 所对的边分别为为
所对的边分别为为 ,
, ,
,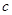 ,且
,且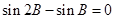
 ,
,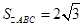 ,求
,求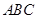 中,角
中,角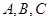 所对的边分别为
所对的边分别为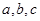 ,已知
,已知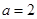 ,
,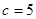 ,
,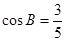 .
.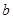 的值;
的值; 的值.
的值.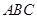 中,角
中,角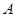 、
、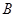 、
、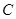 所对的边长分别为
所对的边长分别为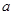 、
、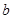 、
、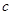 ,
,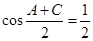 .
. ,
,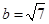 ,求
,求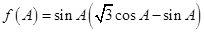 ,求
,求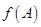 的取值范围.
的取值范围.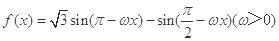 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为 .
. 的值;
的值; 中,
中,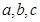 分别是角
分别是角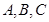 的对边,且
的对边,且 ,求
,求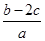 的取值范围.
的取值范围.