题目内容
3．设集合A={（x，y）|logax+logay＞0}，B={（x，y）|y+x＜a}，若A∩B=∅，则a的取值范围是（ ）| A． | ∅ | B． | a＞0，a≠1 | C． | 0＜a≤2，a≠1 | D． | 1＜a≤2 |
分析 利用对数的运算性质化简集合A，然后画出图形，数形结合求得使A∩B=∅的a的取值范围．
解答 解：∵logax+logay=logaxy＞0=loga1，
当a＞1时，有xy＞1，∴y$＞\frac{1}{x}$；
当0＜a＜1时，有0＜xy＜1，∴y$＜\frac{1}{x}$．
（1）当0＜a＜1时，y=$\frac{1}{x}$与y+x＜a的区域始终由公共点，∴0＜a＜1（舍），
；
（2）当a＞1时，要使A∩B=∅，需有x+y=a刚切过（1，1）时，即a=2时成立，
将此直线向左下平移也成立．
∴1＜a≤2，
．
故选：D．
点评 此题考查了简单的线性规划，考查交集及其运算，体现了数形结合的数学思想方法及数学转化思想方法，是中档题．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
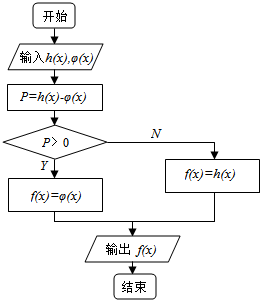函数f（x）的定义由程序框图给出，程序运行时，输入h（x）=（$\frac{1}{2}$）x，φ（x）=log2x，则f（$\frac{1}{2}$）+f（4）的值为-$\frac{15}{16}$．
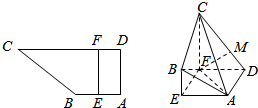如图所示，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD=$\frac{1}{2}$CD=2，点E在边AB上，点F在边CD上，且EF∥AD，沿EF将面EBCF折起，使得CF⊥AE．
15．正四棱锥P-ABCD内接于球，底面ABCD是和球心O在同一平面内，球的体积为$\frac{8\sqrt{2}π}{3}$，则正四棱锥P-ABCD的表面积为 （ ）
| A． | 4$\sqrt{3}$ | B． | 4+4$\sqrt{3}$ | C． | 4+4$\sqrt{2}$ | D． | 4+8$\sqrt{3}$ |
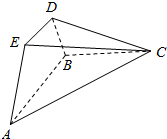已知△ABC为直角三角形，AB⊥BC，四边形ABDE为等腰梯形，DE∥AB，平面ABDE⊥平面ABC，AB=BC=2DE=2．