题目内容
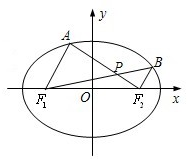 (2012•江苏)如图,在平面直角坐标系xOy中,椭圆
(2012•江苏)如图,在平面直角坐标系xOy中,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆的方程;
(2)设A,B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行,AF2与BF1交于点P.
(i)若AF1-BF2=
| ||
| 2 |
(ii)求证:PF1+PF2是定值.
分析:(1)根据椭圆的性质和已知(1,e)和(e,
),都在椭圆上列式求解.
(2)(i)设AF1与BF2的方程分别为x+1=my,x-1=my,与椭圆方程联立,求出|AF1|、|BF2|,根据已知条件AF1-BF2=
,用待定系数法求解;
(ii)利用直线AF1与直线BF2平行,点B在椭圆上知,可得PF1=
×(2
-BF2),PF2=
×(2
-AF1),由此可求得PF1+PF2是定值.
| ||
| 2 |
(2)(i)设AF1与BF2的方程分别为x+1=my,x-1=my,与椭圆方程联立,求出|AF1|、|BF2|,根据已知条件AF1-BF2=
| ||
| 2 |
(ii)利用直线AF1与直线BF2平行,点B在椭圆上知,可得PF1=
| AF1 |
| AF1+BF2 |
| 2 |
| BF2 |
| AF1+BF2 |
| 2 |
解答:(1)解:由题设知a2=b2+c2,e=
,由点(1,e)在椭圆上,得
+
=1,∴b=1,c2=a2-1.
由点(e,
)在椭圆上,得
+
=1
∴
+
=1,∴a2=2
∴椭圆的方程为
+y2=1.
(2)解:由(1)得F1(-1,0),F2(1,0),
又∵直线AF1与直线BF2平行,∴设AF1与BF2的方程分别为x+1=my,x-1=my.
设A(x1,y1),B(x2,y2),y1>0,y2>0,
∴由
,可得(m2+2)y12-2my1-1=0.
∴y1=
,y1=
(舍),
∴|AF1|=
×|0-y1|=
①
同理|BF2|=
②
(i)由①②得|AF1|-|BF2|=
,∴
=
,解得m2=2.
∵注意到m>0,∴m=
.
∴直线AF1的斜率为
=
.
(ii)证明:∵直线AF1与直线BF2平行,∴
=
,即PF1=
×BF1.
由点B在椭圆上知,BF1+BF2=2
,∴PF1=
×(2
-BF2).
同理PF2=
×(2
-AF1).
∴PF1+PF2=
×(2
-BF2)+
×(2
-AF1)=2
-
由①②得,AF1+BF2=
,AF1×BF2=
,
∴PF1+PF2=
.
∴PF1+PF2是定值.
| c |
| a |
| 1 |
| a2 |
| c2 |
| a2b2 |
由点(e,
| ||
| 2 |
| e2 |
| a2 |
| 3 |
| 4 b2 |
∴
| a2-1 |
| a4 |
| 3 |
| 4 |
∴椭圆的方程为
| x2 |
| 2 |
(2)解:由(1)得F1(-1,0),F2(1,0),
又∵直线AF1与直线BF2平行,∴设AF1与BF2的方程分别为x+1=my,x-1=my.
设A(x1,y1),B(x2,y2),y1>0,y2>0,
∴由
|
∴y1=
m+
| ||
| m2+2 |
m-
| ||
| m2+2 |
∴|AF1|=
| m2+1 |
| ||||
| m2+2 |
同理|BF2|=
| ||||
| m2+2 |
(i)由①②得|AF1|-|BF2|=
2 m
| ||
| m2+2 |
2 m
| ||
| m2+2 |
| ||
| 2 |
∵注意到m>0,∴m=
| 2 |
∴直线AF1的斜率为
| 1 |
| m |
| ||
| 2 |
(ii)证明:∵直线AF1与直线BF2平行,∴
| PB |
| PF1 |
| BF2 |
| AF1 |
| AF1 |
| AF1+BF2 |
由点B在椭圆上知,BF1+BF2=2
| 2 |
| AF1 |
| AF1+BF2 |
| 2 |
同理PF2=
| BF2 |
| AF1+BF2 |
| 2 |
∴PF1+PF2=
| AF1 |
| AF1+BF2 |
| 2 |
| BF2 |
| AF1+BF2 |
| 2 |
| 2 |
| 2AF1×BF2 |
| AF1+BF2 |
由①②得,AF1+BF2=
2
| ||
| m2+2 |
| m2+1 |
| m2+2 |
∴PF1+PF2=
3
| ||
| 2 |
∴PF1+PF2是定值.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
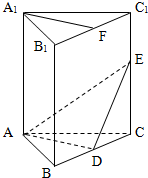 (2012•江苏)如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证:
(2012•江苏)如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证: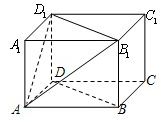 (2012•江苏)如图,在长方体ABCD-A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A-BB1D1D的体积为
(2012•江苏)如图,在长方体ABCD-A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A-BB1D1D的体积为 (2012•江苏)如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-
(2012•江苏)如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-