题目内容
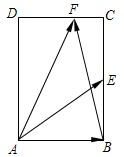
（2012•江苏）如图，在矩形ABCD中，AB=
，BC=2，点E为BC的中点，点F在边CD上，若
•
=
，则
•
的值是
．
| 2 |
| AB |
| AF |
| 2 |
| AE |
| BF |
| 2 |
| 2 |
分析：根据所给的图形，把已知向量用矩形的边所在的向量来表示，做出要用的向量的模长，表示出要求得向量的数量积，注意应用垂直的向量数量积等于0，得到结果．
解答：解：∵
=
+
，
•
=
•(
+
)=
•
+
•
=
•
=
|
|=
，
∴|
|=1，|
|=
-1，
∴
•
=（
+
）（
+
）=
•
+
•
=-
(
-1)+1×2=-2+
+2=
，
故答案为：
| AF |
| AD |
| DF |
| AB |
| AF |
| AB |
| AD |
| DF |
| AB |
| AD |
| AB |
| DF |
| AB |
| DF |
| 2 |
| DF |
| 2 |
∴|
| DF |
| CF |
| 2 |
∴
| AE |
| BF |
| AB |
| BE |
| BC |
| CF |
| AB |
| CF |
| BE |
| BC |
| 2 |
| 2 |
| 2 |
| 2 |
故答案为：
| 2 |
点评：本题考查平面向量的数量积的运算．本题解题的关键是把要用的向量表示成已知向量的和的形式，本题是一个中档题目．
练习册系列答案
相关题目
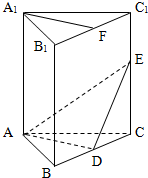（2012•江苏）如图，在直三棱柱ABC-A1B1C1中，A1B1=A1C1，D，E分别是棱BC，CC1上的点（点D 不同于点C），且AD⊥DE，F为B1C1的中点．求证：
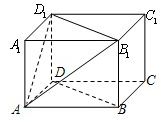（2012•江苏）如图，在长方体ABCD-A1B1C1D1中，AB=AD=3cm，AA1=2cm，则四棱锥A-BB1D1D的体积为
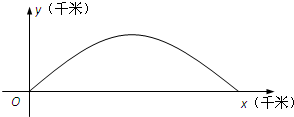（2012•江苏）如图，建立平面直角坐标系xOy，x轴在地平面上，y轴垂直于地平面，单位长度为1千米．某炮位于坐标原点．已知炮弹发射后的轨迹在方程y=kx-
（2012•江苏）如图，在平面直角坐标系xOy中，椭圆