题目内容
.(本题满分15分)已知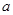 为常数,函数
为常数,函数 (
( )。
)。
(Ⅰ)
若函数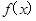 在区间(-2,-1)上为减函数,求实数
在区间(-2,-1)上为减函数,求实数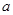 的取值范围;
的取值范围;
(Ⅱ).设
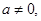 记函数
记函数 ,已知函数
,已知函数 在区间
在区间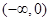 内有两个极值点
内有两个极值点 ,且
,且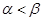 ,若对于满足条件的任意实数
,若对于满足条件的任意实数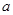 都有
都有 (
(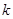 为正整数),求
为正整数),求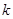 的最小值。
的最小值。
【答案】
(Ⅰ) 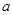 的取值范围是
的取值范围是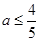 ; (Ⅱ)
; (Ⅱ) 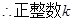 的最小值为2。
的最小值为2。
【解析】 本试题主要是考查了导数在研究函数中的运用,根据已知中的函数求解导数,根据单调性确定参数的范围,以及极值的问题的综合运用。
(1)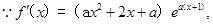 …….1分
…….1分
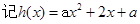
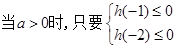 ,解得
,解得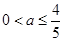
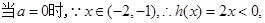 ……4分
……4分
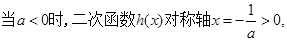
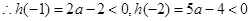 分类讨论的得到结论。
分类讨论的得到结论。
(2)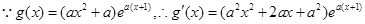
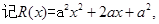
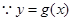 在区间
在区间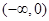 内有两个极值点
内有两个极值点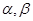 ,
,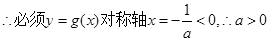 ,
,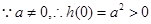 ,只要
,只要
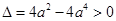 ,解得
,解得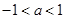 ,
,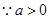
 ,然后分析得到。
,然后分析得到。
解(Ⅰ) 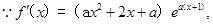 …….1分
…….1分
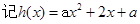
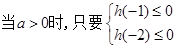 ,解得
,解得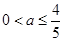 ,……..3分
,……..3分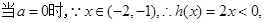 ……4分
……4分
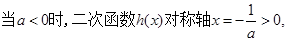
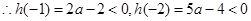 ,
,
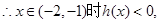 5分
5分
综合上得,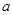 的取值范围是
的取值范围是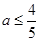 ….7分
….7分
(Ⅱ)
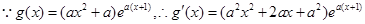
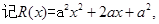
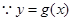 在区间
在区间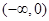 内有两个极值点
内有两个极值点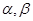 ,
,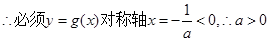 ,
,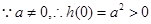 ,只要
,只要
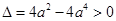 ,解得
,解得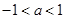 ,
,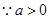
 …..9分
…..9分
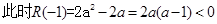
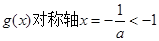 ,
,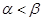
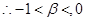
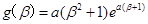 ,
,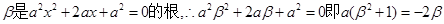
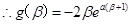 ,……11分
,……11分
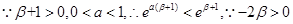
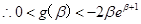 ,设
,设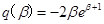
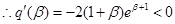
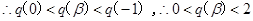 ,
,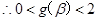 ……..13分
……..13分
又因存在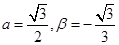 ,
,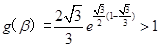 ,此时
,此时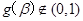
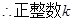 的最小值为2。…….15分(未举例说明
的最小值为2。…….15分(未举例说明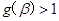 扣1分)
扣1分)

练习册系列答案
相关题目
 .
. 在
在 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数 的最大值;
的最大值; 对任意的
对任意的 ,
, 都成立,求实数
都成立,求实数 的取值范围.
的取值范围. 为自然对数的底数.
为自然对数的底数. 与曲线
与曲线 相切
相切 在
在 上恰有两个不等的实数根
上恰有两个不等的实数根 ,求
,求 的大小
的大小 :
: (
( ),焦点为
),焦点为 ,直线
,直线 交抛物线
交抛物线 、
、 两点,
两点, 是线段
是线段 的中点,
的中点, 轴的垂线交抛物线
轴的垂线交抛物线 ,
, 到焦点
到焦点 ,求此时
,求此时 的值;
的值; 是以
是以

 的单调区间;
的单调区间; ,若
,若 在
在 上不单调且仅在
上不单调且仅在 处取得最大值,求
处取得最大值,求 的取值范围.
的取值范围.