题目内容
如图的几何体中, 平面
平面 ,
, 平面
平面 ,△
,△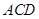 为等边三角形,
为等边三角形,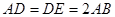 ,
,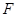 为
为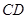 的中点.
的中点.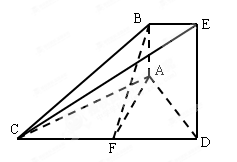
(1)求证: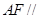 平面
平面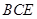 ;
;
(2)求证:平面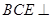 平面
平面 .
.
证明见解析.
解析试题分析:(1)要证线面平行,关键是在平面内找一条与待证直线平行的直线,本题中,由于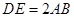 ,
,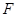 是中点,故很容易让人联想到取另一中点,这里我们取
是中点,故很容易让人联想到取另一中点,这里我们取 中点
中点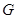 ,则
,则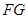 ∥
∥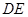 ∥
∥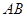 ,
,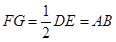 ,故
,故 是平行四边形,从而有
是平行四边形,从而有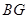 ∥
∥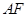 ,平行线找到了,结论得证;(2)要证面垂直,就是要证线面垂直,关键是找哪个平面内的直线,同样本题里由于
,平行线找到了,结论得证;(2)要证面垂直,就是要证线面垂直,关键是找哪个平面内的直线,同样本题里由于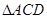 是等边三角形,故
是等边三角形,故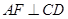 ,从而很快得到结论
,从而很快得到结论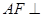 平面
平面 ,而(1)中有
,而(1)中有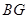 ∥
∥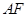 ,则有
,则有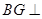 平面
平面 ,这就是我们要的平面的垂线,由此就证得了面面垂直.
,这就是我们要的平面的垂线,由此就证得了面面垂直.
试题解析:(1)证明:取 的中点
的中点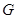 ,连结
,连结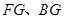 .
.
∵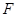 为
为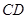 的中点,∴
的中点,∴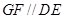 且
且 .
.
∵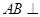 平面
平面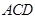 ,
,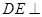 平面
平面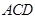 ,
,
∴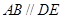 ,∴
,∴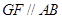 . 又
. 又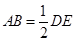 ,∴
,∴ .
.
∴四边形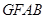 为平行四边形,则
为平行四边形,则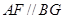 .
.
∵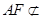 平面
平面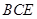 ,
,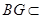 平面
平面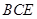 , ∴
, ∴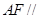 平面
平面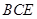 . 7分
. 7分
(2)证明:∵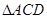 为等边三角形,
为等边三角形,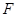 为
为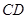 的中点,∴
的中点,∴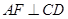
∵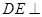 平面
平面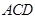 ,
,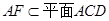 ,∴
,∴ .
.
∵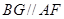 ,∴
,∴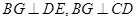 又
又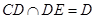 ,
,
∴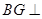 平面
平面 .
.
∵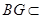 平面
平面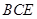 , ∴平面
, ∴平面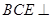 平面
平面 . 14分
. 14分
考点:(1)线面平行;(2)面面垂直.

练习册系列答案
相关题目
 所在平面与正
所在平面与正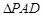 所在平面互相垂直,
所在平面互相垂直,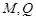 分别为
分别为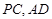 的中点.
的中点.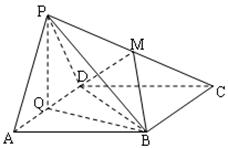
 平面
平面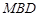 ;
;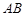 上是否存在一点
上是否存在一点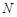 ,使得平面
,使得平面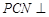 平面
平面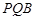 ?若存在,试指出点
?若存在,试指出点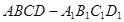 中,
中,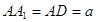 ,
, , E、
, E、 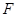 分别为
分别为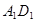 、
、 的中点.
的中点.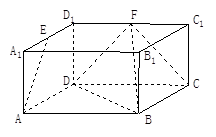
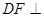 平面
平面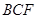 ;
;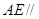 平面
平面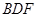 .
.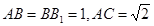 ,直线B1C与平面ABC成45°角.
,直线B1C与平面ABC成45°角.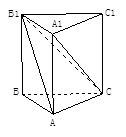
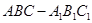 中,
中,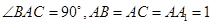 ,
,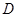 是棱
是棱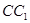 上的一点,
上的一点, 是
是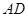 的延长线与
的延长线与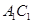 的延长线的交点,且
的延长线的交点,且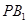 ∥平面
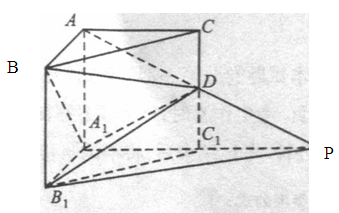
∥平面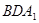 。
。
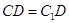 ;
;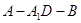 的平面角的余弦值;
的平面角的余弦值;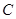 到平面
到平面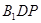 的距离.
的距离.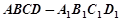 中,已知平面
中,已知平面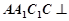 平面
平面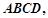 且
且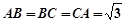 ,
,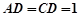 .
.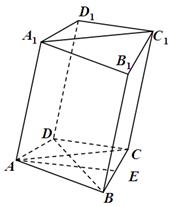
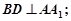
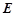 为棱
为棱 的中点,求证:
的中点,求证: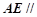 平面
平面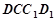 .
. 的底面
的底面 是平行四边形,且
是平行四边形,且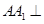 底面
底面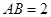 ,
,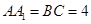 ,
,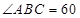 °,点
°,点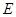 为
为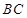 中点,点
中点,点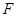 为
为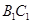 中点.
中点.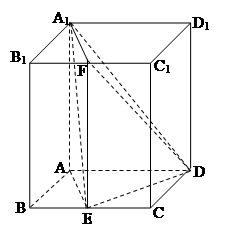
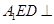 平面
平面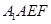 ;
;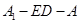 的大小为
的大小为 ,直线
,直线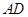 与平面
与平面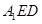 所成的角为
所成的角为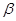 ,求
,求 的值.
的值.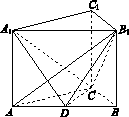
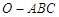 的侧棱
的侧棱 两两垂直,且
两两垂直,且 ,
,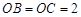 ,
, 是
是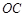 的中点。
的中点。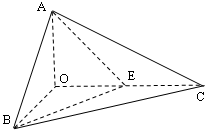
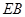 与
与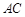 所成角的余弦值;
所成角的余弦值;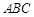 的所成角的正弦值。
的所成角的正弦值。