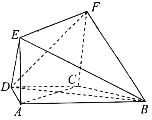
题目内容
【题目】在平面直角坐标系![]() 中,已知椭圆E:
中,已知椭圆E:![]() (
(![]() )过点
)过点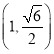 ,其心率等于
,其心率等于![]() .
.
(1)求椭圆E的标准方程;
(2)若A,B分别是椭圆E的左,右顶点,动点M满足![]() ,且
,且![]() 椭圆E于点P.
椭圆E于点P.
①求证:![]() 为定值:
为定值:
②设![]() 与以
与以![]() 为直径的圆的另一交点为Q,求证:直线
为直径的圆的另一交点为Q,求证:直线![]() 经过定点.
经过定点.
【答案】(1)![]() ;(2)①见解析,②见解析.
;(2)①见解析,②见解析.
【解析】
(1)由题意的离心率公式和点满足题意方程,结合椭圆的![]() ,
,![]() ,
,![]() 的关系解出方程,进而得到椭圆方程;
的关系解出方程,进而得到椭圆方程;
(2)①设![]() ,
,![]() ,求得直线
,求得直线![]() 的方程,代入椭圆方程,解得点
的方程,代入椭圆方程,解得点![]() 的坐标,再由向量的数量积的坐标表示,计算即可得证;
的坐标,再由向量的数量积的坐标表示,计算即可得证;
②先求得![]() 的斜率,再由圆的性质可得
的斜率,再由圆的性质可得![]() ,求出
,求出![]() 的斜率,再求直线
的斜率,再求直线![]() 的方程,即可得到定点.
的方程,即可得到定点.
(1)设椭圆焦距为![]() ,所以
,所以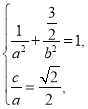 且
且![]()
解得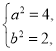
所以椭圆E的方程为![]() ;
;
(2)设![]() ,
,![]() ,
,
①易得直线![]() 的方程为:
的方程为:![]() ,
,
代入椭圆![]() 得,
得, ,
,
由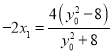 得,
得,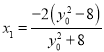 ,从而
,从而![]() ,
,
所以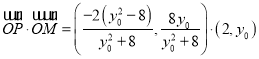
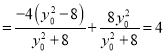 .
.
②依题意,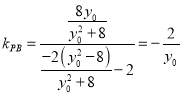 ,
,
由![]() 得,
得,![]() ,
,
则![]() 的方程为:
的方程为:![]() ,即
,即![]() ,
,
所以直线![]() 过定点
过定点![]() .
.

【题目】某科研小组对冬季昼夜温差大小与某反季节作物种子发芽多少之间的关系进行分析,分别记录了每天昼夜温差和每100颗种子的发芽数,其中5天的数据如下,该小组的研究方案是:先从这5组数据中选取3组求线性回归方程,再用方程对其余的2组数据进行检验.
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
温度 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 26 | 32 | 26 | 16 |
(1)求余下的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是第2、3、4天的数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与2组检验数据的误差均不超过1颗,则认为得到的线性回归方程是可靠的,请问(2)中所得的线性回归方程是否可靠?
(参考公式;线性回归方程![]() 中系数计算公式:
中系数计算公式: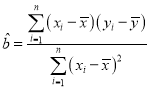
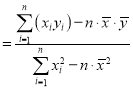 ,
,![]() ,其中
,其中![]() 、
、![]() 表示样本的平均值)
表示样本的平均值)
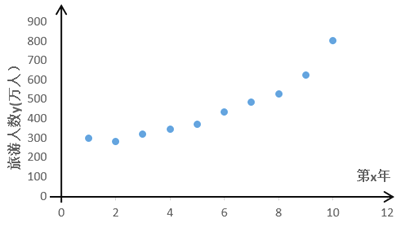
【题目】某景区的各景点从2009年取消门票实行免费开放后,旅游的人数不断地增加,不仅带动了该市淡季的旅游,而且优化了旅游产业的结构,促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变.下表是从2009年至2018年,该景点的旅游人数![]() (万人)与年份
(万人)与年份![]() 的数据:
的数据:
第 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
旅游人数 | 300 | 283 | 321 | 345 | 372 | 435 | 486 | 527 | 622 | 800 |
该景点为了预测2021年的旅游人数,建立了![]() 与
与![]() 的两个回归模型:
的两个回归模型:
模型①:由最小二乘法公式求得![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ;
;
模型②:由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近.
的附近.
(1)根据表中数据,求模型②的回归方程![]() .(
.(![]() 精确到个位,
精确到个位,![]() 精确到0.01).
精确到0.01).
(2)根据下列表中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
回归方程 | ① | ② |
| 30407 | 14607 |
参考公式、参考数据及说明:
①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为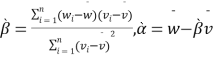 .②刻画回归效果的相关指数
.②刻画回归效果的相关指数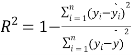 ;③参考数据:
;③参考数据:![]() ,
,![]() .
.
|
|
|
|
|
|
5.5 | 449 | 6.05 | 83 | 4195 | 9.00 |
表中![]() .
.