题目内容

8．已知等比数列{an}中，8a2+a5=0，则$\frac{S_4}{S_2}$=（　　）
A．-2B．1C．2D．5

分析 由已知可得q=-2，代入等比数列前n项和公式，求出S2，S4，可得答案．

解答 解：∵等比数列{an}中，8a2+a5=0，
∴等比数列{an}中，8a2+q3a2=0，
解得：q=-2，
∴S2=-a1，S4=-5a1，
∴$\frac{{S}_{4}}{{S}_{2}}$=5，
故选：D．

点评 本题考查的知识点是等比数列前n项和公式，难度不大，属于基础题．

练习册系列答案
相关题目
18．f（x）=-2x2+mx-3在（-∞，3]上是增函数，则实数m的取值范围是（　　）
A．{1，2}B．[6，+∞）C．[12，+∞）D．（-∞，6]
19．数据5，7，7，8，10，11的方差是（　　）
A．24B．10C．4D．2
16．一个盒子中装有标号为1，2，3，4，5的5个球，同时选取两个球，则两个球上的数字为相邻整数的概率为$\frac{2}{5}$．
3．已知f（x）=$\left\{\begin{array}{l}{a{x}^{2}+x}&{x≥0}\\{-a{x}^{2}+x}&{x＜0}\end{array}\right.$，当x∈[-$\frac{1}{4}$，$\frac{1}{4}$]时恒有f（x+a）＜f（x），则实数a的取值范围是（　　）
A．（$\frac{1-\sqrt{17}}{4}，0$）B．[-2，0）C．（-∞，-$\sqrt{2}$）D．[-2，-$\sqrt{2}$]
13．若正方形三条边所在直线方程是：2x+y-1=0，2x+y+1=0，x-2y-1=0，则第四条边直线所在方程是x-2y+1=0或x-2y-3=0．
20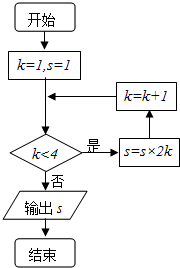．执行如图所示的程序框图，输出的s值为（　　）
A．8B．16C．48D．64
17．设x，y满足$\left\{\begin{array}{l}{x-y+5≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$，求①μ=x2+y2，求最大值和最小值；②μ=$\frac{y}{x-5}$，求最大值和最小值．
18．已知集合 A={0，1，2}，B={1，m}，若 A∩B=B，则实数m的值是0或2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网