题目内容
已知m>0,a,b∈R,求证: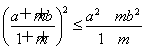 .
.
见解析
【解析】因为m>0,所以1+m>0,
所以要证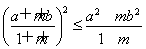 ,
,
即证(a+mb)2≤(1+m)(a2+mb2),
即证m(a2-2ab+b2)≥0,
即证(a-b)2≥0,
而(a-b)2≥0显然成立,
故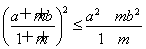 .
.

练习册系列答案
相关题目
题目内容
已知m>0,a,b∈R,求证: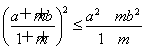 .
.
见解析
【解析】因为m>0,所以1+m>0,
所以要证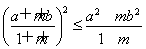 ,
,
即证(a+mb)2≤(1+m)(a2+mb2),
即证m(a2-2ab+b2)≥0,
即证(a-b)2≥0,
而(a-b)2≥0显然成立,
故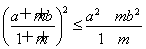 .
.
