题目内容
已知点E,F的坐标分别是(-2,0)、(2,0),直线EP,FP相交于点P,且它们的斜率之积为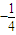 .
.(1)求证:点P的轨迹在椭圆
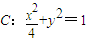 上;
上;(2)设过原点O的直线AB交(1)题中的椭圆C于点A、B,定点M的坐标为
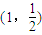 ,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;
,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;(3)某同学由(2)题结论为特例作推广,得到如下猜想:
设点M(a,b)(ab≠0)为椭圆
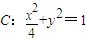 内一点,过椭圆C中心的直线AB与椭圆分别交于A、B两点.则当且仅当kOM=-kAB时,△MAB的面积取得最大值.
内一点,过椭圆C中心的直线AB与椭圆分别交于A、B两点.则当且仅当kOM=-kAB时,△MAB的面积取得最大值.问:此猜想是否正确?若正确,试证明之;若不正确,请说明理由.
【答案】分析:(1)由已知中点E,F的坐标分别是(-2,0)、(2,0),直线EP,FP相交于点P,且它们的斜率之积为 .我们设出P(x,y),进而得到x,y之间的关系式,整理后即可得到点P的轨迹方程.
.我们设出P(x,y),进而得到x,y之间的关系式,整理后即可得到点P的轨迹方程.
(2)设直线AB的方程为y=kx,A(x1,kx1),则B(-x1,-kx1),联立直线和椭圆的方程,我们可得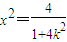 ,利用弦定公式,求出AB的长,利用点到直线公式,求出M点直线AB的距离求出AB边的高,可以得到△MAB面积的表达式,进而求出△MAB面积m的取值范围,得到△MAB面积m的,代入可求出对应的k值.
,利用弦定公式,求出AB的长,利用点到直线公式,求出M点直线AB的距离求出AB边的高,可以得到△MAB面积的表达式,进而求出△MAB面积m的取值范围,得到△MAB面积m的,代入可求出对应的k值.
(3)设M(1,4),根据(2)的计算办法,我们易求出,△MAB的面积取得最大值时,并求出此进kOM及kAB的值,验证后,可得猜想不成立.
解答:证明:(1)设P(x,y),由直线PE,PF的斜率均存在可知,x≠±2
由题意可得,
整理可得, (x≠±2)
(x≠±2)
点P的轨迹为椭圆 上
上
(2)设直线AB的方程为y=kx,A(x1,kx1),则B(-x1,-kx1)
联立方程
整理可得
AB=2OA=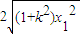 =
=
∵M( )到直线AB的距离d=
)到直线AB的距离d=
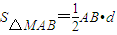 =
= =m
=m
则4(1-m2)k2-4k+1-m2=0
则42-4•4(1-m2)•(1-m2)≥0
即(1-m2)2≤1
又由m≥0可得
0≤m≤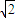
即三角形MAB的最大值为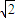
代入4(1-m2)k2-4k+1-m2=0得
k=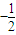
(3)设M(1, ),则M点在椭圆
),则M点在椭圆 内
内
由(2)中推导过程,可得
当k0M= ,kAB=-1时,△MAB的面积取得最大值
,kAB=-1时,△MAB的面积取得最大值
此时kOM≠-kAB,
故猜想:点M(a,b)(ab≠0)为椭圆 内一点,
内一点,
过椭圆C中心的直线AB与椭圆分别交于A、B两点.
则当且仅当kOM=-kAB时,△MAB的面积取得最大值正确
点评:本题考查的知识点是直线与圆锥曲线的综合问题,其中(1)的关键是分别求出两条直线的斜率,进而得到P点横、纵坐标的关系式,(2)的关键是得到△MAB面积的表达式,(3)中正面证明比较麻烦,可以举出一反例,推反前面的猜想.
 .我们设出P(x,y),进而得到x,y之间的关系式,整理后即可得到点P的轨迹方程.
.我们设出P(x,y),进而得到x,y之间的关系式,整理后即可得到点P的轨迹方程.(2)设直线AB的方程为y=kx,A(x1,kx1),则B(-x1,-kx1),联立直线和椭圆的方程,我们可得
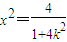 ,利用弦定公式,求出AB的长,利用点到直线公式,求出M点直线AB的距离求出AB边的高,可以得到△MAB面积的表达式,进而求出△MAB面积m的取值范围,得到△MAB面积m的,代入可求出对应的k值.
,利用弦定公式,求出AB的长,利用点到直线公式,求出M点直线AB的距离求出AB边的高,可以得到△MAB面积的表达式,进而求出△MAB面积m的取值范围,得到△MAB面积m的,代入可求出对应的k值.(3)设M(1,4),根据(2)的计算办法,我们易求出,△MAB的面积取得最大值时,并求出此进kOM及kAB的值,验证后,可得猜想不成立.
解答:证明:(1)设P(x,y),由直线PE,PF的斜率均存在可知,x≠±2
由题意可得,

整理可得,
 (x≠±2)
(x≠±2)点P的轨迹为椭圆
 上
上(2)设直线AB的方程为y=kx,A(x1,kx1),则B(-x1,-kx1)
联立方程

整理可得

AB=2OA=
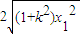 =
=
∵M(
 )到直线AB的距离d=
)到直线AB的距离d=
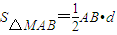 =
= =m
=m则4(1-m2)k2-4k+1-m2=0
则42-4•4(1-m2)•(1-m2)≥0
即(1-m2)2≤1
又由m≥0可得
0≤m≤
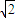
即三角形MAB的最大值为
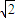
代入4(1-m2)k2-4k+1-m2=0得
k=
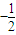
(3)设M(1,
 ),则M点在椭圆
),则M点在椭圆 内
内由(2)中推导过程,可得
当k0M=
 ,kAB=-1时,△MAB的面积取得最大值
,kAB=-1时,△MAB的面积取得最大值此时kOM≠-kAB,
故猜想:点M(a,b)(ab≠0)为椭圆
 内一点,
内一点,过椭圆C中心的直线AB与椭圆分别交于A、B两点.
则当且仅当kOM=-kAB时,△MAB的面积取得最大值正确
点评:本题考查的知识点是直线与圆锥曲线的综合问题,其中(1)的关键是分别求出两条直线的斜率,进而得到P点横、纵坐标的关系式,(2)的关键是得到△MAB面积的表达式,(3)中正面证明比较麻烦,可以举出一反例,推反前面的猜想.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
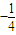 .
.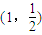 ,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;
,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;