题目内容
9.(实验班做)(1)已知sinα-sinβ=-$\frac{1}{3}$,cosα-csoβ=$\frac{1}{2}$,求cos(α-β)=$\frac{59}{72}$.(写出计算过程)
(2)在△ABC中,已知tanA,tanB是方程3x2-7x+2=0的两个实根,求tanC?
分析 (1)把所给的2个条件平方,利用同角三角函数的基本关系求得cosαcosβ+sinαsinβ 的值,可得cos(α-β)=cosαcosβ+sinαsinβ 的值.
(2)由条件利用韦达定理求得tanA+tanB和tanA•tanB的值,可得tan(A+B)的值,进而求得tanC=-tan(A+B)的值.
解答 解:(1)∵已知sinα-sinβ=-$\frac{1}{3}$,cosα-csoβ=$\frac{1}{2}$,
∴平方可得 1-2sinαsinβ=$\frac{1}{9}$,1-2cosαcosβ=$\frac{1}{4}$,
∴2-2sinαsinβ-2cosαcosβ=$\frac{1}{9}+\frac{1}{4}$=$\frac{13}{36}$,
即cosαcosβ+sinαsinβ=$\frac{59}{72}$,
由此求得 cos(α-β)=cosαcosβ+sinαsinβ=$\frac{59}{72}$,
故答案为:$\frac{59}{72}$.
(2)在△ABC中,
∵已知tanA,tanB是方程3x2-7x+2=0的两个实根,
∴tanA+tanB=$\frac{7}{3}$,tanA•tanB=$\frac{2}{3}$,
∴tan(A+B)=$\frac{tanA+tanB}{1-tanA•tanB}$=7,
∴tanC=-tan(A+B)=-7.
点评 本题主要考查同角三角函数的基本关系,韦达定理,两角和差的三角公式,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.直线经过A(2,1),B(1,m2)两点(m∈R),那么直线l的倾斜角的取值范围是( )
| A. | [0,π) | B. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,π) | C. | [0,$\frac{π}{4}$] | D. | [$\frac{π}{4}$,$\frac{π}{2}$)∪($\frac{π}{2}$,π) |
18.如图所示的是一串黑白相间排列的珠子,若按这种规律排列下去,那么第34颗珠子的颜色是( )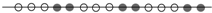
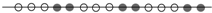
| A. | 白色 | B. | 白色的可能性大 | C. | 黑色 | D. | 黑色的可能性大 |
 已知椭圆C1:$\frac{x^2}{4}+{y^2}$=1的左、右焦点分别是F1、F2,Q是椭圆外的动点,满足|$\overrightarrow{{F_1}Q}$|=4.点P是线段F1Q与该椭圆C1的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|≠0.
已知椭圆C1:$\frac{x^2}{4}+{y^2}$=1的左、右焦点分别是F1、F2,Q是椭圆外的动点,满足|$\overrightarrow{{F_1}Q}$|=4.点P是线段F1Q与该椭圆C1的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|≠0.