��Ŀ����
����Ŀ��ij��λ�⽨һ���Ȼ���״�Ļ�̳����ͼ��ʾ���������Ҫ���Ȼ����ܳ�Ϊ30�ף����д�Բ������Բ�İ뾶Ϊ10�ף���СԲ������Բ�İ뾶Ϊx�ף�Բ�Ľ�Ϊ�ȣ����ȣ��� 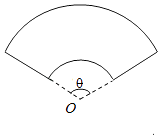
��1����ȹ���x�ĺ�����ϵʽ��
��2����֪�Ի�̳�ı�Ե��ʵ�߲��֣�����װ��ʱ��ֱ�߲��ֵ�װ�η���Ϊ4Ԫ/�ף����߲��ֵ�װ�η���Ϊ9Ԫ/�ף��軨̳�������װ���ܷ���֮��Ϊy����y����x�ĺ�����ϵʽ�������y�����ֵ��
���𰸡�
��1���⣺�����֪30=�ȣ�10+x��+2��10��x�������Ԧ�= ![]() ��x�ʣ�0��10��
��x�ʣ�0��10��
��2���⣺��̳�����Ϊ ![]() �ȣ�102��x2��=��5+x����10��x��=��x2+5x+50��0��x��10����
�ȣ�102��x2��=��5+x����10��x��=��x2+5x+50��0��x��10����
װ���ܷ���Ϊ9�ȣ�10+x��+8��10��x��=170+10x��
���Ի�̳�������װ���ܷ���֮��Ϊy= ![]() =��
=�� ![]() ��
��
��t=17+x��t�ʣ�17��27����y= ![]() ��
�� ![]() ��t+
��t+ ![]() ����
���� ![]() ��
�� ![]() =
= ![]() ��
��
���ҽ���t=18ʱȡ�Ⱥţ���ʱx=1����= ![]() ��
��
��������˫����������������ֵ�ģ���ͬ�ȱ����֣�����˵�������ԣ���
�ʵ�x=1ʱ����̳�������װ���ܷ���֮�����
����������1���������ε��ܳ���ʽ������⼴�ɣ���2����ϻ�̳�������ʽ����Ϸ���֮��Ĺ�ϵ������⼴�ɣ�

����Ŀ��ij��ҵ����A��B���ֲ�Ʒ������ÿһ�ֲ�Ʒ������Ͷ�����ú�͵�������
��ƷƷ�� | �Ͷ��������� | ú���֣� | �磨ǧ�ߣ� |
A��Ʒ | 3 | 9 | 4 |
B��Ʒ | 10 | 4 | 5 |
��֪����ÿ��A��Ʒ��������7��Ԫ������ÿ��B��Ʒ��������12��Ԫ�������������ƣ�����ҵ�����Ͷ���300����ú360�֣����ҹ����ֻ�ܹ���200ǧ�ߣ����ʸ���ҵ��ΰ������������ܻ���������