题目内容
如图，已知直线l1：4x+y=0，直线l2：x+y-1=0以及l2上一点P（3，-2）．求有圆心在l1上且与直线l2相切于点P的圆的方程．分析：由已知可设圆心坐标为（m，-4m），进而由圆与直线l2相切于点P，则圆心到直线l2的距离与圆心到点P的距离相等，构造方程，解方程求出圆心坐标，进而可得圆的标准方程
解答：解：∵圆心在l1上，直线l1：4x+y=0，
∴设圆心坐标为（m，-4m）
又∵圆与直线l2相切于点P，直线l2：x+y-1=0以及点P（3，-2）．
∴
=
即m2-2m+1=0
解得m=1
故圆心坐标为（1，-4）、
圆的半径r满足r2=（m-3）2+（-4m+2）2=8
故所求圆的方程为（x-1）2+（y+4）2=8
∴设圆心坐标为（m，-4m）
又∵圆与直线l2相切于点P，直线l2：x+y-1=0以及点P（3，-2）．
∴
| |m-4m-1| | ||
|
| (m-3)2+(-4m+2)2 |
即m2-2m+1=0
解得m=1
故圆心坐标为（1，-4）、
圆的半径r满足r2=（m-3）2+（-4m+2）2=8
故所求圆的方程为（x-1）2+（y+4）2=8
点评：本题考查的知识点是圆的标准方程，其中根据已知结合圆心到直线l2的距离与圆心到点P的距离相等，构造方程，是解答的关键．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
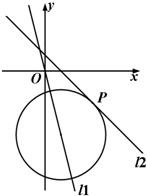如图，已知直线l1：4x+y=0，直线l2：x+y-1=0以及l2上一点P（3，-2）．
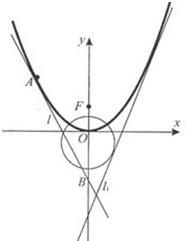如图，已知直线l1：y=2x+m（m＜0）与抛物线C1：y=ax2（a＞0）和圆C2：x2+（y+1）2=5都相切，F是C1的焦点．
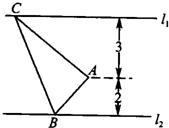如图，已知直线l1∥l2，点A是l1，l2之间的定点，点A到l1，l2之间的距离分别为3和2，点B是l2上的一动点，作AC⊥AB，且AC与l1交于点C，则△ABC的面积的最小值为
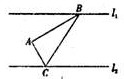如图，已知直线l1∥l2，点A是l1，l2上两直线之间的动点，且到l1距离为4，到l2距离为3，若