��Ŀ����
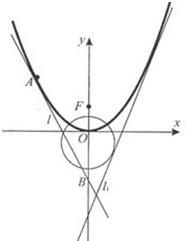 ��ͼ����ֱ֪��l1��y=2x+m��m��0����������C1��y=ax2��a��0����ԲC2��x2+��y+1��2=5�����У�F��C1�Ľ��㣮
��ͼ����ֱ֪��l1��y=2x+m��m��0����������C1��y=ax2��a��0����ԲC2��x2+��y+1��2=5�����У�F��C1�Ľ��㣮��1����m��a��ֵ��
��2����A��C1�ϵ�һ���㣬��AΪ�е���������C1������l��ֱ��l��y���ڵ�B����FA��FBΪ�ڱ���ƽ���ı���FAMB��֤������M��һ����ֱ���ϣ�
��3���ڣ�2���������£��ǵ�M���ڵĶ�ֱ��Ϊl2��ֱ��l2��y�ύ��ΪN������MF��������C1��P��Q���㣬���NPQ�����S��ȡֵ��Χ��
��������1������Բ�ĵ�ֱ�ߵľ�����ڰ뾶���m�������õ����������ߵĹ�ϵ���a��ֵ���ɣ�
��2���������AΪ�е������l�ķ����Լ���A��B�ı���ʽ����������FA��FBΪ�ڱ���ƽ���ı���FAMB������������㼴�������M���ڵĶ�ֱ�ߣ�
��3����ֱ��MF��y=kx+
������y=
x2�ã�
x2-kx-
=0����ϸ���ϵ���Ĺ�ϵ�������������ʽ�ó�����ı���ʽ��������ú���˼�뼴����á�NPQ�����S��ȡֵ��Χ��
��2���������AΪ�е������l�ķ����Լ���A��B�ı���ʽ����������FA��FBΪ�ڱ���ƽ���ı���FAMB������������㼴�������M���ڵĶ�ֱ�ߣ�
��3����ֱ��MF��y=kx+
| 3 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| 3 |
| 2 |
����⣺��1������֪��ԲC2��x2+��y+1��2=5��Բ��ΪC2��0��-1�����뾶 r=
����1�֣�
������Բ�ĵ�ֱ��l1��y=2x+m�ľ��� d=
����3�֣�
��
=
��
���m=-6��m=4��ȥ������4�֣�
��l1�������ߵ����е�ΪA0��x0��y0������y��=2ax����5�֣�
�� 2ax0=2?x0=
��y0=
����6�֣�
����ֱ�߷��̵ã�
=
-6����a=
����m=-6��a=
����7�֣�
��2���ɣ�1��֪������C1����Ϊ y=
x2������ F(0��
)����8�֣�
�� A(x1��
)���ɣ�1��֪��AΪ�е������l�ķ���Ϊ y=
x1(x-x1)+
����10�֣�
��x=0��������l��y���B������Ϊ (0��-
)��11�֣�
����
=(x1��
-
)��
=(0��-
-
)����12�֣�
��
=
+
=(x1��-3)��13�֣�
��ΪF�Ƕ��㣬���Ե�M�ڶ�ֱ�� y=-
�ϣ���14�֣�
��3����ֱ��MF��y=kx+
������y=
x2�ã�
x2-kx-
=0����x1+x2=6k��x1x2=-9��
S��NPQ=
|NF||x1-x2|=
��3��
=9
��k��0����S��NPQ��9��
��NPQ�����S��ȡֵ��Χ��9��+�ޣ���
| 5 |
������Բ�ĵ�ֱ��l1��y=2x+m�ľ��� d=
| |1+m| | ||
|
��
| |1+m| | ||
|
| 5 |
���m=-6��m=4��ȥ������4�֣�
��l1�������ߵ����е�ΪA0��x0��y0������y��=2ax����5�֣�
�� 2ax0=2?x0=
| 1 |
| a |
| 1 |
| a |
����ֱ�߷��̵ã�
| 1 |
| a |
| 2 |
| a |
| 1 |
| 6 |
����m=-6��a=
| 1 |
| 6 |
��2���ɣ�1��֪������C1����Ϊ y=
| 1 |
| 6 |
| 3 |
| 2 |
�� A(x1��
| 1 |
| 6 |
| x | 2 1 |
| 1 |
| 3 |
| 1 |
| 6 |
| x | 2 1 |
��x=0��������l��y���B������Ϊ (0��-
| 1 |
| 6 |
| x | 2 1 |
����
| FA |
| 1 |
| 6 |
| x | 2 1 |
| 3 |
| 2 |
| FB |
| 1 |
| 6 |
| x | 2 1 |
| 3 |
| 2 |
��
| FM |
| FA |
| FB |
��ΪF�Ƕ��㣬���Ե�M�ڶ�ֱ�� y=-
| 3 |
| 2 |
��3����ֱ��MF��y=kx+
| 3 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| 3 |
| 2 |
S��NPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| (x 1+x 2) 2 -4x 1x 2 |
| 1+k2 |
��k��0����S��NPQ��9��
��NPQ�����S��ȡֵ��Χ��9��+�ޣ���
�����������Ƕ�Բ����Բ֪ʶ���ۺϿ��飮��ֱ����Բ����ʱ����������Բ�ĵ�ֱ�ߵľ�����ڰ뾶��⣮��Ҳ����ֱ����Բ�ķ��������ö�Ӧ���̵��б�ʽΪ0��⣮�����õ��ǵ�һ��

��ϰ��ϵ�д�
 �ο�������ϵ�д�
�ο�������ϵ�д� ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�����Ŀ
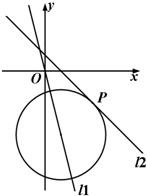 ��ͼ����ֱ֪��l1��4x+y=0��ֱ��l2��x+y-1=0�Լ�l2��һ��P��3��-2����
��ͼ����ֱ֪��l1��4x+y=0��ֱ��l2��x+y-1=0�Լ�l2��һ��P��3��-2���� ��ͼ����ֱ֪��l1��4x+y=0��ֱ��l2��x+y-1=0�Լ�l2��һ��P��3��-2��������Բ����l1������ֱ��l2�����ڵ�P��Բ�ķ��̣�
��ͼ����ֱ֪��l1��4x+y=0��ֱ��l2��x+y-1=0�Լ�l2��һ��P��3��-2��������Բ����l1������ֱ��l2�����ڵ�P��Բ�ķ��̣�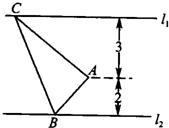 ��ͼ����ֱ֪��l1��l2����A��l1��l2֮��Ķ��㣬��A��l1��l2֮��ľ���ֱ�Ϊ3��2����B��l2�ϵ�һ���㣬��AC��AB����AC��l1���ڵ�C�����ABC���������СֵΪ
��ͼ����ֱ֪��l1��l2����A��l1��l2֮��Ķ��㣬��A��l1��l2֮��ľ���ֱ�Ϊ3��2����B��l2�ϵ�һ���㣬��AC��AB����AC��l1���ڵ�C�����ABC���������СֵΪ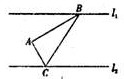 ��ͼ����ֱ֪��l1��l2����A��l1��l2����ֱ��֮��Ķ��㣬�ҵ�l1����Ϊ4����l2����Ϊ3����
��ͼ����ֱ֪��l1��l2����A��l1��l2����ֱ��֮��Ķ��㣬�ҵ�l1����Ϊ4����l2����Ϊ3����