题目内容
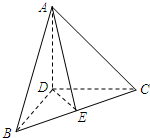如图，在三棱锥A-BCD中，DA，DB，DC两两垂直，且DB=DC，E为BC中点，则| AE |
| BC |
（ ）
| A、0 | B、1 | C、2 | D、3 |
分析：根据两个要求数量积的向量的位置，把这两个向量用以D为起点的向量来表示，整理出含有向量的数量积的表示形式，根据垂直和长度关系得到结果．
解答：解：∵
•
=
(
+
)•(
-
)
=
(
-
+
-
)• (
-
)
=
(
- 2
+
)• (
-
)
=
•
-
2-
•
+
•
+
2-
•
∵DA，DB，DC两两垂直，且DB=DC，
∴
•
=0
故选A．
| AE |
| BC |
| 1 |
| 2 |
| AB |
| AC |
| DC |
| DB |
=
| 1 |
| 2 |
| DB |
| DA |
| DC |
| DA |
| DC |
| DB |
=
| 1 |
| 2 |
| DB |
| DA |
| DC |
| DC |
| DB |
=
| 1 |
| 2 |
| DB |
| DC |
| 1 |
| 2 |
| DB |
| DA |
| DC |
| DA |
| DB |
| 1 |
| 2 |
| DC |
| 1 |
| 2 |
| DC |
| DB |
∵DA，DB，DC两两垂直，且DB=DC，
∴
| AE |
| BC |
故选A．
点评：本题考查空间向量的数量积的运算，本题解题的关键是把要求数量积的向量表示成已知向量的和或差的形式，再进行数量积的运算．
练习册系列答案
相关题目
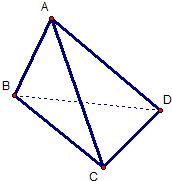如图，在三棱锥A-BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜边，且AD=
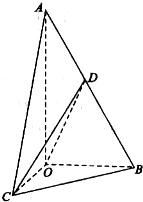如图，在三棱锥A-BOC中，AO⊥底面BOC，∠OAB=∠OAC=30°，AB=AC=4，
如图，在三棱锥A-BCD中，AD⊥平面ABC，∠BAC=120°，且AB=AC=AD=2，点E在BC上，且AE⊥AC．
如图，在三棱锥A-BOC中，AO⊥面BOC，二面角B-AO-C是直二面角，OB=OC，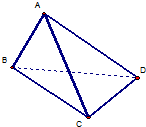
如图，在三棱锥A-BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜边，且AD=