题目内容
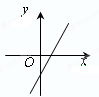
已知函数f(x)=x2+bx+c的导函数y=f′(x)的图象如图所示,且f(x)满足b2-4c>0,那么f(x)的顶点所在的象限为( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |

由函数f(x)=x2+bx+c的二次项系数大于0,所以对应的图象为开口向上的抛物线,二次函数有最小值,且最小值就是极小值,又由f′(x)=2x+b,且导函数的图象交x轴于正半轴,所以-
>0,即原函数顶点的横坐标大于0,
再由f(x)满足b2-4c>0,说明顶点在x轴下方.
综上可知,f(x)的顶点所在的象限为第四象限.
故选D.
| b |
| 2 |
再由f(x)满足b2-4c>0,说明顶点在x轴下方.
综上可知,f(x)的顶点所在的象限为第四象限.
故选D.

练习册系列答案
相关题目
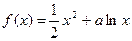 (a∈R).(1)若
(a∈R).(1)若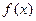 在[1,e]上是增函数,求a的取值范围(2)若a=1,a≤x≤e,证明:
在[1,e]上是增函数,求a的取值范围(2)若a=1,a≤x≤e,证明: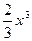
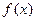 的定义域为[—2,
的定义域为[—2,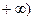 ,部分对应值如下表。
,部分对应值如下表。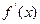 为
为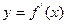 的图象如右图所示:
的图象如右图所示: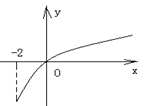
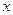
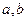 满足
满足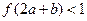 ,则
,则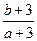 的取值范围是( )
的取值范围是( )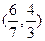
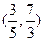
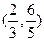
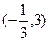
 在区间
在区间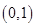 上单调递增,且方程
上单调递增,且方程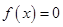 的根都在区间
的根都在区间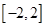 上,则实数b的取值范围为( )
上,则实数b的取值范围为( )