题目内容
（本题满分12分）
已知函数f（x）=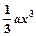
-bx2+（2-b）x+1在x=x1处取得极大值，在x=x2处取得极小值，且0<x1<1<x2<2
(1) 当x1=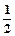
,x2=
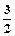时,求a,b的值;
（2）若w=2a+b,求w的取值范围;
已知函数f（x）=
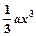-bx2+（2-b）x+1在x=x1处取得极大值，在x=x2处取得极小值，且0<x1<1<x2<2(1) 当x1=
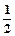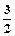,x2=时,求a,b的值;（2）若w=2a+b,求w的取值范围;
(1)
;
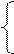
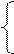(2)f/(x)=ax2-2bx+2-b,由题意得: f/(0)>0 2-b>0
f/(1)<0 得 a-3b+2<0
f/(2)>0 4a-5b+2>0
可行域为(如图)
A(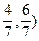
B（4，2）C（2，2）
由此可得w的取值范围是（2，10）
; (2)f/(x)=ax2-2bx+2-b,由题意得: f/(0)>0 2-b>0f/(1)<0 得 a-3b+2<0
f/(2)>0 4a-5b+2>0
可行域为(如图)
A(
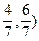B（4，2）C（2，2）由此可得w的取值范围是（2，10）
略
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
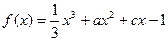在区间（1，2）单调递减。
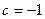时，求a的取值范围；
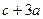的取值范围。
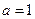时，求函数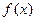
的单调增区间，求函数
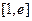上的最小值；
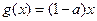，若存在
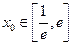，使得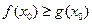
成立，求实数
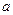的取值范围。
的最大值为M，最小值为m，则M+m的值为( )
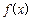的导函数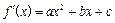
的图象如右图，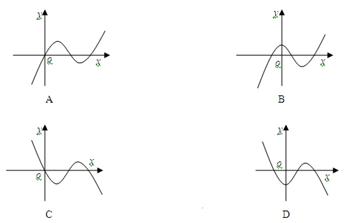
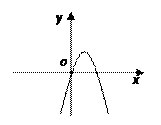
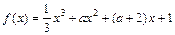有极大值和极小值，则a的取值范围为 .
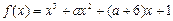有极大值和极小值，则
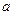的取值范围是 .
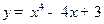在区间[－2,3 ]上的最小值为 ( )