题目内容
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处导数相等,证明:
处导数相等,证明:![]() ;
;
(2)若对于任意![]() ,直线
,直线![]() 与曲线
与曲线![]() 都有唯一公共点,求实数
都有唯一公共点,求实数![]() 的取值范围.
的取值范围.
【答案】(I)见解析(II)![]()
【解析】
(1)由题x>0,![]() ,由f(x)在x=x1,x2(x1≠x2)处导数相等,得到
,由f(x)在x=x1,x2(x1≠x2)处导数相等,得到![]() ,得
,得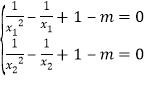 ,
,
由韦达定理得![]() ,由基本不等式得
,由基本不等式得![]() ,得
,得![]() ,由题意得
,由题意得![]() ,令
,令![]() ,则
,则![]() ,令
,令![]() ,,利用导数性质能证明
,,利用导数性质能证明![]() .
.
(2)由![]() 得
得![]() ,令
,令![]() ,
,
利用反证法可证明证明![]() 恒成立。
恒成立。
由对任意![]() ,
,![]() 只有一个解,得
只有一个解,得![]() 为
为![]() 上的递增函数,
上的递增函数,![]() 得
得![]() ,令
,令![]() ,由此可求
,由此可求![]() 的取值范围..
的取值范围..
(I)![]()
令![]() ,得
,得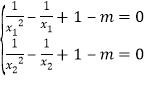 ,
,
由韦达定理得![]()
即![]() ,得
,得![]()
![]()
![]()
令![]() ,则
,则![]() ,令
,令![]() ,
,
则![]() ,得
,得![]()
(II)由![]() 得
得![]()
令![]() ,
,
则![]() ,
,![]() ,
,![]()
下面先证明![]() 恒成立。
恒成立。
若存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,且当自变量
,且当自变量![]() 充分大时,
充分大时,![]() ,所以存在
,所以存在![]() ,
,![]() ,使得
,使得![]() ,
,![]() ,取
,取![]() ,则
,则![]() 与
与![]() 至少有两个交点,矛盾。
至少有两个交点,矛盾。
由对任意![]() ,
,![]() 只有一个解,得
只有一个解,得![]() 为
为![]() 上的递增函数,
上的递增函数,![]()
得![]() ,令
,令![]() ,则
,则![]() ,
,
得![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目