题目内容
已知直线l:y=mx+4,圆C:x2+y2=4.
(1)若直线l与圆C相切,求实数m的值和直线l的方程;
(2)若直线l与圆C相离,求实数m的取值范围.
(1)若直线l与圆C相切,求实数m的值和直线l的方程;
(2)若直线l与圆C相离,求实数m的取值范围.
分析:方法一:求出圆心到直线的距离,(1)直线l与圆C相切,则d=r;(2)直线l与圆C相离,则d>r,利用点到直线的距离公式,可求相应的值;
方法二:把直线l:y=mx+4方程代入圆C:x2+y2=4,可得一元二次方程,(1)若直线l与圆C相切,则△=0;(2)若直线l与圆C相离,则△<0,可求相应的值.
方法二:把直线l:y=mx+4方程代入圆C:x2+y2=4,可得一元二次方程,(1)若直线l与圆C相切,则△=0;(2)若直线l与圆C相离,则△<0,可求相应的值.
解答:解:(方法一)直线l方程为mx-y+4=0,到圆心C(0,0)的距离d=
.
又圆C的半径r=2.…(3分)
(1)若直线l与圆C相切,则d=r,即
=2.…(5分)
解得m2=3,所以m=±
.…(7分)
所以直线l方程为
x-y+4=0或
x+y-4=0.…(8分)
(2)若直线l与圆C相离,则d>r,即
>2.…(10分)
解得m2<3,所以-
<m<
,即m的取值范围是(-
,
).…(12分)
(方法二)把直线l:y=mx+4方程代入圆C:x2+y2=4,得(m2+1)x2+8mx+12=0,…(3分)
其判别式△=(8m)2-4×12×(m2+1).…(5分)
(1)若直线l与圆C相切,则△=0,解得m2=3,所以m=±
.…(7分)
所以直线l方程为
x-y+4=0或
x+y-4=0.…(8分)
(2)若直线l与圆C相离,则△<0.…(10分)
解得m2<3,所以-
<m<
,即m的取值范围是(-
,
).…(12分)
| |4| | ||
|
又圆C的半径r=2.…(3分)
(1)若直线l与圆C相切,则d=r,即
| |4| | ||
|
解得m2=3,所以m=±
| 3 |
所以直线l方程为
| 3 |
| 3 |
(2)若直线l与圆C相离,则d>r,即
| |4| | ||
|
解得m2<3,所以-
| 3 |
| 3 |
| 3 |
| 3 |
(方法二)把直线l:y=mx+4方程代入圆C:x2+y2=4,得(m2+1)x2+8mx+12=0,…(3分)
其判别式△=(8m)2-4×12×(m2+1).…(5分)
(1)若直线l与圆C相切,则△=0,解得m2=3,所以m=±
| 3 |
所以直线l方程为
| 3 |
| 3 |
(2)若直线l与圆C相离,则△<0.…(10分)
解得m2<3,所以-
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题考查直线与圆的位置关系,考查代数法语几何法是运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
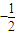 ,求此抛物线的方程.
,求此抛物线的方程.