题目内容
已知直线l:y=mx+1与曲线C:ax2+y2=2(m,a∈R)交于A、B两点.
(1)当m=0时,有∠AOB=
,求曲线P的方程;
(2)是否存在常数M,使得对于任意的a∈(0,1),m∈R,都有
•
<M恒成立?如果存在,求出的M得最小值;如果不存在,说明理由.
(1)当m=0时,有∠AOB=
| π |
| 3 |
(2)是否存在常数M,使得对于任意的a∈(0,1),m∈R,都有
| OA |
| OB |
分析:(1)直线方程为y=1,代入曲线C:ax2+y2=2求得A,B的坐标,利用∠AOB=
可求曲线的方程;
(2)将直线l:y=mx+1与曲线C:ax2+y2=2联立,化简得(a+m2)x2+2mx-1=0,假设点A,B的坐标,利用
=
+1,求得对于任意的a∈(0,1),m∈R,它的最大值小于2,故取M的值大于2时,都有
•
<M恒成立,故存在常数M,使得对于任意的a∈(0,1),m∈R,都有
•
<M恒成立且M得最小值为:2.
| π |
| 3 |
(2)将直线l:y=mx+1与曲线C:ax2+y2=2联立,化简得(a+m2)x2+2mx-1=0,假设点A,B的坐标,利用
| OA |
| m2-1 |
| m2+a |
| OA |
| OB |
| OA |
| OB |
解答:解:(1)由题意,直线方程为y=1,代入曲线C:ax2+y2=2可得 A(-
,1),B(
,1),
∵∠AOB=
,∴tan
=
,∴a=3
∴曲线C的方程为3x2+y2=2.
(2)将直线l:y=mx+1与曲线C:ax2+y2=2联立,化简得(a+m2)x2+2mx-1=0
设A(x1,y1),B(x2,y2),则知 x1+x2=-
,x1x2=-
,
∴
•
=x1x2+y1y2=
+(mx1+1)(mx2+1)=
+1=2+
,
对于任意的a∈(0,1),m∈R,
•
的最大值小于2.
∴取M大于等于2时,都有
•
<M恒成立,
故存在M,使得对于任意的a∈(0,1),m∈R,都有
•
<M恒成立,且M的最小值为2.
|
|
∵∠AOB=
| π |
| 3 |
| π |
| 6 |
|
∴曲线C的方程为3x2+y2=2.
(2)将直线l:y=mx+1与曲线C:ax2+y2=2联立,化简得(a+m2)x2+2mx-1=0
设A(x1,y1),B(x2,y2),则知 x1+x2=-
| 2m |
| m2+a |
| 1 |
| m2+a |
∴
| OA |
| OB |
| -1 |
| m2+a |
| m2-1 |
| m2+a |
| 1-a |
| m2+a |
对于任意的a∈(0,1),m∈R,
| OA |
| OB |
∴取M大于等于2时,都有
| OA |
| OB |
故存在M,使得对于任意的a∈(0,1),m∈R,都有
| OA |
| OB |
点评:本题考查直线与圆锥曲线的综合问题,解题的关键是结合韦达定理,利用函数思想分析求解.

练习册系列答案
相关题目
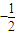 ,求此抛物线的方程.
,求此抛物线的方程.