题目内容
已知直线l:y=mx+1与曲线C:ax2+y2=2(m、a∈R)交于A、B两点,O为坐标原点.
(1)当m=0时,有∠AOB=
,求曲线C的方程;
(2)当实数a为何值时,对任意m∈R,都有
•
为定值T?指出T的值;
(3)已知点M(0,-1),当a=-2,m变化时,动点P满足
=
+
,求动点P的纵坐标的变化范围.
(1)当m=0时,有∠AOB=
| π |
| 3 |
(2)当实数a为何值时,对任意m∈R,都有
| OA |
| OB |
(3)已知点M(0,-1),当a=-2,m变化时,动点P满足
| MP |
| OA |
| OB |
分析:(1)当m=0时,推出A,B的坐标,利用∠AOB=
,求出a的值,即可得到曲线C的方程;
(2)设A、B两点坐标为(x1,y1)、(x2,y2),联立方程,通过韦达定理结合
•
的表达式为定值T,即可求出a的值以及T的值;
(3)设出动点P,求出
=
+
,结合(2)求出y=
,通过判别式求出m的范围,即可求动点P的纵坐标的变化范围.
| π |
| 3 |
(2)设A、B两点坐标为(x1,y1)、(x2,y2),联立方程,通过韦达定理结合
| OA |
| OB |
(3)设出动点P,求出
| MP |
| OA |
| OB |
| 2+m2 |
| 2-m2 |
解答:解:(1)当m=0时,联立方程可得:ax2=1,∴x=±
∴A(
,1),B(-
,1),∵∠AOB=
,∴
=
解得:a=3,
∴方程为
+
=1
(2)设A、B两点坐标为(x1,y1)、(x2,y2),联立方程:
可得:
(a+m2)x2+2mx-1=0
∴
∴
•
=x1x2+y1y2=x1x2+(mx1+1)(mx2+1)=(m2+1)x1x2+m(x1+x2)+1=-
-
+1=
要使
•
=T,则-2m2+(a-1)=Tm2+Ta∴T=-2且a-1=Ta即a=
且T=-2
而当a=
时,
+m2≠0且△=4m2+4(
+m2)=8m2+
>0恒成立∴当实数a=
时,对任意m∈R,都有
•
=-2
(3)设P(x,y),∴
=(x,y+1),∴y+1=y1+y2=m(x1+x2)+2=
∴y=
又对方程(m2-2)x2+2mx-1=0,△=8m2-8>0,∴m2>1且m2≠2
∴y=-1+
,∴y>3或y<-1
|
∴A(
|
|
| π |
| 3 |
| 1 |
| 2 |
-
| ||
|
∴方程为
| 3x2 |
| 2 |
| y2 |
| 2 |
(2)设A、B两点坐标为(x1,y1)、(x2,y2),联立方程:
|
(a+m2)x2+2mx-1=0
∴
|
∴
| OA |
| OB |
| m2+1 |
| a+m2 |
| 2m2 |
| a+m2 |
| a-2m2-1 |
| a+m2 |
要使
| OA |
| OB |
| 1 |
| 3 |
而当a=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| OA |
| OB |
(3)设P(x,y),∴
| MP |
| 4 |
| 2-m2 |
| 2+m2 |
| 2-m2 |
又对方程(m2-2)x2+2mx-1=0,△=8m2-8>0,∴m2>1且m2≠2
∴y=-1+
| 4 |
| 2-m2 |
点评:本题难题,考查曲线的轨迹方程的求法,韦达定理的应用,向量的数量积的计算以及判别式的应用,考查计算能力,转化思想,整体思想的应用,变量范围问题一般通过一个等式与一个不等式求解.

练习册系列答案
相关题目
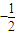 ,求此抛物线的方程.
,求此抛物线的方程.