题目内容
14.若实数x、y满足$\left\{\begin{array}{l}{2x+y-2≥0}\\{y≤3}\\{3x-4y-3≤0}\end{array}\right.$,则x2-2xy+y2的取值范围是[0,$\frac{49}{4}$].分析 画出满足满足$\left\{\begin{array}{l}{2x+y-2≥0}\\{y≤3}\\{3x-4y-3≤0}\end{array}\right.$的平面区域,利用角点法求出Z=x-y的范围,进而得到x2-2xy+y2的取值范围.
解答 解:满足$\left\{\begin{array}{l}{2x+y-2≥0}\\{y≤3}\\{3x-4y-3≤0}\end{array}\right.$的平面区域如下图所示: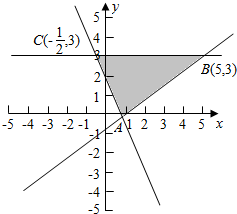
令Z=x-y,
则ZA=1,ZB=2,ZC=$-\frac{7}{2}$,
即Z∈[$-\frac{7}{2}$,2],
故x2-2xy+y2=Z2∈[0,$\frac{49}{4}$],
故答案为:[0,$\frac{49}{4}$]
点评 在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.

练习册系列答案
相关题目
9.已知等比数列{an}满足a1+a2=3,a2+a3=6,则a2014=( )
| A. | 22013 | B. | 22014 | C. | 32013 | D. | 32014 |
3.设U=Z,M={x|x=2k,k∈Z},P={x|x=3k,k∈Z},则M∩(CUP)=( )
| A. | {x|x=3k±1,k∈Z} | B. | {x|x=4k±1,k∈Z} | C. | {x|x=6k±2,k∈Z} | D. | {x|x=4k或4k+2,k∈Z} |