题目内容
已知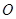 为坐标原点,向量
为坐标原点,向量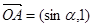 ,
,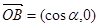 ,
,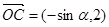 ,点
,点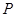 满足
满足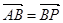 .
.
(Ⅰ)记函数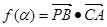 ,
,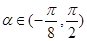 ,讨论函数
,讨论函数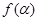 的单调性,并求其值域;
的单调性,并求其值域;
(Ⅱ)若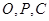 三点共线,求
三点共线,求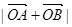 的值.
的值.
(Ⅰ)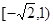 ;(Ⅱ)
;(Ⅱ)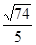 .
.
解析试题分析:(Ⅰ)设点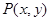 ,利用向量的数量积及函数
,利用向量的数量积及函数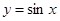 的性质求解;(Ⅱ)由
的性质求解;(Ⅱ)由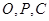 三点共线,转化为向量共线,根据三角函数公式、变换求出
三点共线,转化为向量共线,根据三角函数公式、变换求出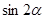 ,再求向量的模..
,再求向量的模..
试题解析:(Ⅰ)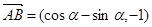 ,设
,设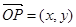 ,则
,则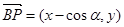 ,
,
由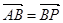 得
得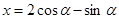 ,
,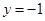 ,
,
故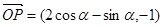 ,
,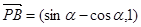 ,
,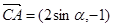 ,
,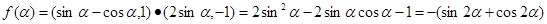
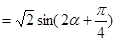 , (3分)
, (3分)
又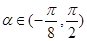 ,
,
故函数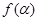 的单调递增区间为
的单调递增区间为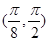 ,单调递减区间为
,单调递减区间为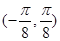 ,
,
因为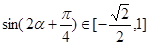 ,故函数
,故函数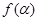 的值域为
的值域为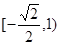 . (6分)
. (6分)
(Ⅱ)由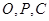 三点共线可得
三点共线可得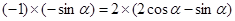 得
得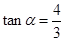 ,(9分)
,(9分)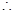
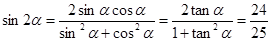 ,
,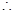
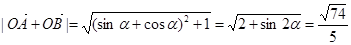 . (12分)
. (12分)
考点:三角函数的性质,两角和的正、余弦公式和向量基本定理,三角恒等变换.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 中,角
中,角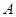 ,
,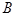 ,
,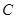 所对的边分别为
所对的边分别为 ,
,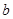 ,
,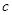 ,且
,且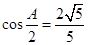 .
.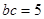 ,求
,求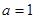 ,求
,求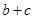 的最大值.
的最大值. 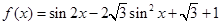 .
. 的最小正周期;
的最小正周期;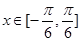 时,求
时,求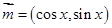 和
和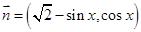 ,
,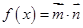 ,写出函数
,写出函数 的最小正周期;并求函数
的最小正周期;并求函数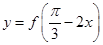 的单调区间;
的单调区间;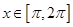 ,求
,求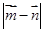 的最大值.
的最大值. 的图象过点(0,
的图象过点(0,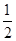 ),最小正周期为
),最小正周期为 ,且最小值为-1.
,且最小值为-1. 的解析式.
的解析式. ,
, ,求m的取值范围.
,求m的取值范围.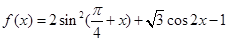 .
.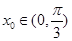 ,使f(x0)=1,求x0的值;
,使f(x0)=1,求x0的值;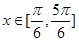 ,条件q:
,条件q: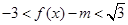 ,若p是q的充分条件,求实数m的取值范围.
,若p是q的充分条件,求实数m的取值范围. ,中心角
,中心角 .求证:当
.求证:当 时该扇形面积最大;
时该扇形面积最大;
 .求证:
.求证: .
.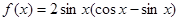 ,其中
,其中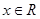
 的最小正周期,并从下列的变换中选择一组合适变换的序号,经过这组变换的排序,可以把函数
的最小正周期,并从下列的变换中选择一组合适变换的序号,经过这组变换的排序,可以把函数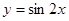 的图像变成
的图像变成 的图像;(要求变换的先后顺序)
的图像;(要求变换的先后顺序)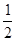 倍,
倍,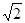 倍,
倍,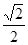 倍,
倍,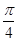 个单位,
个单位,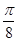 个单位,
个单位,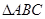 中角
中角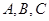 对应边分别为
对应边分别为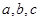 ,
,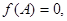
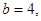
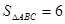 ,求
,求 的长.
的长.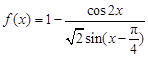 .
. 的定义域;
的定义域;