题目内容
 如图,F为双曲线
如图,F为双曲线| x2 |
| a2 |
| y2 |
| b2 |
分析:由题意求出A,B1,F的坐标,利用∠FB1A=90°,推出a,b,c的关系,即可求出双曲线的离心率.
解答:解:因为双曲线
-
=1的左焦点F(-C,0),A是它的右顶点(a,0),B1B2为虚轴,B1(0,b),
因为∠FB1A=90°,所以AF2=B1F2+B1A2,即:(a+c)2=a2+b2+b2+c2,又c2=a2+b2,
所以ac=c2-a2,e2-e-1=0解得e=
.
故选D.
| x2 |
| a2 |
| y2 |
| b2 |
因为∠FB1A=90°,所以AF2=B1F2+B1A2,即:(a+c)2=a2+b2+b2+c2,又c2=a2+b2,
所以ac=c2-a2,e2-e-1=0解得e=
| ||
| 2 |
故选D.
点评:本题是基础题,考查双曲线的简单性质的应用,注意勾股定理的应用,离心率的范围,考查计算能力.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
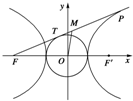 如图,从双曲线
如图,从双曲线| x2 |
| a2 |
| y2 |
| b2 |
| A、|MO|-|MT|>b-a |
| B、|MO|-|MT|<b-a |
| C、|MO|-|MT|=b-a |
| D、以上三种可能都有 |
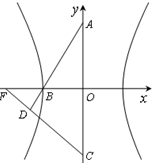 如图,已知双曲线x2-
如图,已知双曲线x2-| y2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
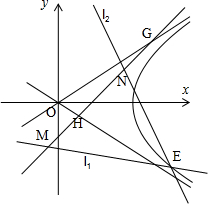
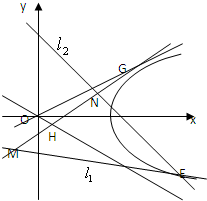
 如图,过双曲线
如图,过双曲线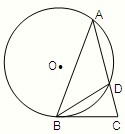 请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.
请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.