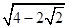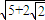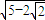题目内容
 如图,过双曲线
如图,过双曲线| x2 |
| 16 |
| y2 |
| 25 |
分析:根据三角形的中位线性质,双曲线的定义,及圆的切线性质,即可得到结论.
解答: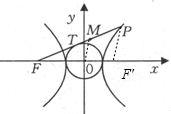 解:设F'是双曲线的右焦点,连接PF'.
解:设F'是双曲线的右焦点,连接PF'.
∵M、O分别为FP、FF'的中点,∴|MO|=
|PF'|.
|FT|=
=5,由双曲线定义得,|PF|-|PF'|=8,
故|MO|-|MT|=
|PF'|-|MF|+|FT|=
(|PF'|-|PF|)+|FT|=-4+5=1.
故选A.
 解:设F'是双曲线的右焦点,连接PF'.
解:设F'是双曲线的右焦点,连接PF'.∵M、O分别为FP、FF'的中点,∴|MO|=
| 1 |
| 2 |
|FT|=
| |OF|2-|OT|2 |
故|MO|-|MT|=
| 1 |
| 2 |
| 1 |
| 2 |
故选A.
点评:本题考查圆与双曲线的综合,解题的关键是正确运用双曲线的定义,三角形的中位线性质.

练习册系列答案
相关题目
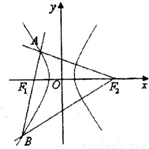
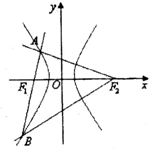 如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若△ABF2是等腰三角形,则双曲线的离心率为( )
如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若△ABF2是等腰三角形,则双曲线的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
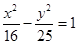 的左焦点F引圆
的左焦点F引圆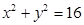 的切线,切点为T,延长FT交双曲线右支于P点,若M为线段FP的中点,O为坐标原点,则|MO|—|MT|=( )
的切线,切点为T,延长FT交双曲线右支于P点,若M为线段FP的中点,O为坐标原点,则|MO|—|MT|=( )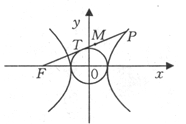
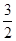 C.
C.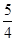 D.2
D.2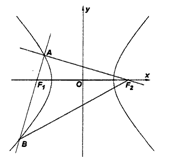
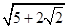 B.
B.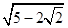 C.
C.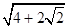 D.
D.