题目内容
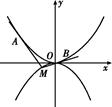
如图,椭圆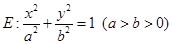 的左焦点为
的左焦点为 ,右焦点为
,右焦点为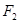 ,过
,过 的直线交椭圆于
的直线交椭圆于 两点,
两点,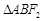 的周长为8,且
的周长为8,且 面积最大时,
面积最大时, 为正三角形.
为正三角形.
(1)求椭圆 的方程;
的方程;
(2)设动直线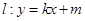 与椭圆
与椭圆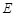 有且只有一个公共点
有且只有一个公共点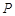 ,且与直线
,且与直线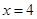 相交于点
相交于点 ,证明:点
,证明:点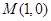 在以
在以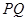 为直径的圆上.
为直径的圆上.
(1)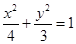 (2)证明过程详见解析
(2)证明过程详见解析
解析试题分析:
(1)利用椭圆的定义,可以得到三角形ABF2的周长即为2a,则可以得到a的值,由椭圆的对称性,可以得到 为正三角形当且仅当A点在椭圆的短轴端点,此时
为正三角形当且仅当A点在椭圆的短轴端点,此时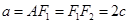 ,则可得到c的值,再根据a,c,b之间的关系可得到b的值,进而得到椭圆E的方程.
,则可得到c的值,再根据a,c,b之间的关系可得到b的值,进而得到椭圆E的方程.
(2)据题意,直线l与椭圆E相切于点P.设出点P的坐标,利用直线与椭圆相切,联立椭圆与直线的方程,判别式为0,即可用点P的坐标表示直线l的斜率,即得到直线l关于P坐标的表达式.联立直线l与直线x=4即可求出点Q的坐标,把P,Q的坐标带入 内积式,证得
内积式,证得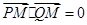
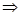
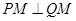 即可.
即可.
试题解析:
(1)由题得,因为点A,B都在椭圆上,所以根据椭圆的定义有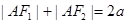 且
且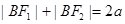 ,又因为
,又因为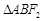 的周长为8,所以
的周长为8,所以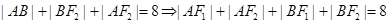
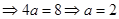 , 因为椭圆是关于x,y,原点对称的,所以
, 因为椭圆是关于x,y,原点对称的,所以 为正三角形当且仅当
为正三角形当且仅当 为椭圆的短轴定点,则
为椭圆的短轴定点,则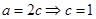 ,
,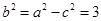 ,故椭圆E的方程为
,故椭圆E的方程为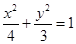 .
.
(2)由题得,动直线l为椭圆的切线,故不妨设切点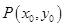 ,因为直线l的斜率是存在且为
,因为直线l的斜率是存在且为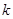 ,所以
,所以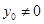 ,则直线
,则直线 ,联立直线l与椭圆E的方程得
,联立直线l与椭圆E的方程得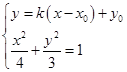
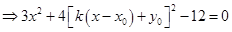 ,
,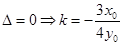 .则直线l的方程为
.则直线l的方程为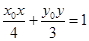 ,联立直线l与直线
,联立直线l与直线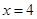 得到点
得到点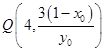 ,则
,则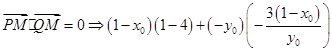
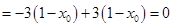 ,所以
,所以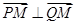 ,即点M在以PQ为直径的圆上.
,即点M在以PQ为直径的圆上.
考点:椭圆 切线 内积 圆

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 时,切线MA的斜率为-
时,切线MA的斜率为- .
.
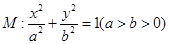 的离心率为
的离心率为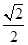 ,且经过点
,且经过点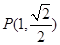 过坐标原点的直线
过坐标原点的直线 与
与 均不在坐标轴上,
均不在坐标轴上,
 =λ,求λ的取值范围.
=λ,求λ的取值范围.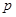 :方程
:方程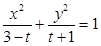 所表示的曲线为焦点在
所表示的曲线为焦点在 轴上的椭圆;命题
轴上的椭圆;命题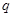 :实数
:实数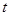 满足不等式
满足不等式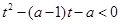 .
. 的取值范围.
的取值范围. .
. =2
=2 ,求△AOB的面积.
,求△AOB的面积.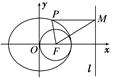
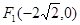 和
和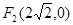 ,长轴长为6,设直线
,长轴长为6,设直线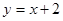 交椭圆C于A、B两点,求线段AB的中点坐标
交椭圆C于A、B两点,求线段AB的中点坐标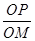 =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线.