题目内容
已知命题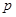 :方程
:方程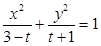 所表示的曲线为焦点在
所表示的曲线为焦点在 轴上的椭圆;命题
轴上的椭圆;命题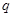 :实数
:实数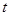 满足不等式
满足不等式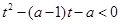 .
.
(1)若命题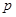 为真,求实数的取值范围;
为真,求实数的取值范围;
(2)若命题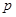 是命题
是命题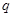 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
(1)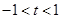 ;(2)
;(2)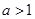 .
.
解析试题分析:(1)命题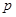 为真应满足
为真应满足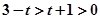 ,解不等式即可求解;(2)本题可转化为满足
,解不等式即可求解;(2)本题可转化为满足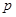 真的
真的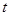 的取值集合,是满足
的取值集合,是满足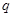 为真的
为真的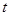 的取值集合的真子集,可以考虑借助二次函数与二次不等式的关系求解.
的取值集合的真子集,可以考虑借助二次函数与二次不等式的关系求解.
试题解析:(1)∵方程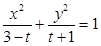 所表示的曲线为焦点在
所表示的曲线为焦点在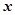 轴上的椭圆
轴上的椭圆
∴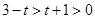
解得: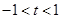
(2)∵命题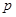 是命题
是命题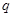 的充分不必要条件
的充分不必要条件
∴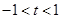 是不等式
是不等式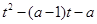 =
=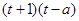
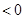 解集的真子集
解集的真子集
法一:因方程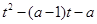 =
=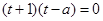 两根为
两根为
故只需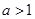
法二:令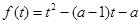 ,因
,因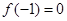 ,故只需
,故只需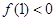
解得: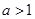 .
.
考点:1.椭圆的标准方程;2.命题真假的判断;3.充分必要条件;4.二次不等式.

练习册系列答案
相关题目
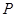 在椭圆
在椭圆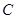 :
: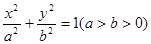 上,以
上,以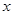 轴相切于椭圆的右焦点
轴相切于椭圆的右焦点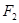 ,且
,且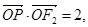
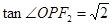 ,其中
,其中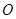 为坐标原点.
为坐标原点. ,设
,设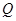 是椭圆
是椭圆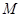 两点的直线
两点的直线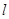 交
交 轴于点
轴于点 ,若
,若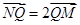 , 求直线
, 求直线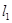 与椭圆
与椭圆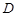 :
: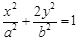 交于不同的两点
交于不同的两点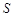 ,
,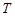 ,其中
,其中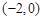 ,若点
,若点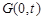 是线段
是线段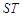 垂直平分线上一点,且满足
垂直平分线上一点,且满足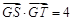 ,求实数
,求实数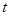 的值.
的值. -
- =1(a>0,b>0)上一点,M,N分别是双曲线E的左,右顶点,直线PM,PN的斜率之积为
=1(a>0,b>0)上一点,M,N分别是双曲线E的左,右顶点,直线PM,PN的斜率之积为 .
.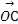 =λ
=λ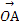 +
+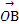 ,求λ的值.
,求λ的值. .过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).
.过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).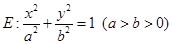 的左焦点为
的左焦点为 ,右焦点为
,右焦点为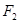 ,过
,过 两点,
两点,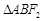 的周长为8,且
的周长为8,且 面积最大时,
面积最大时,
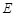 的方程;
的方程;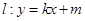 与椭圆
与椭圆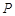 ,且与直线
,且与直线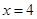 相交于点
相交于点 ,证明:点
,证明:点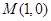 在以
在以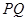 为直径的圆上.
为直径的圆上. +
+ =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为 .
. 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.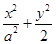 =1(a>
=1(a>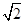 )的右焦点为F1,直线l:x=
)的右焦点为F1,直线l:x=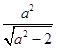 与x轴交于点A,若
与x轴交于点A,若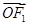 =2
=2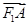 (其中O为坐标原点).
(其中O为坐标原点).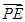 ·
·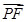 的最大值.
的最大值.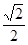 的椭圆
的椭圆 (
( )过点
)过点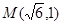
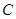 的方程;
的方程;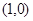 作斜率为
作斜率为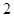 直线
直线 与椭圆相交于
与椭圆相交于 两点,求
两点,求 的长.
的长.