题目内容
设同时满足条件:①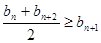 ;②
;②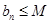 (
(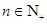 ,
,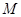 是与
是与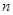 无关的常数)的无穷数列
无关的常数)的无穷数列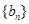 叫“嘉文”数列.已知数列
叫“嘉文”数列.已知数列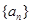 的前
的前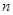 项和
项和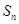 满足:
满足: 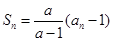 (
(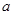 为常数,且
为常数,且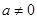 ,
,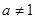 ).
).
(Ⅰ)求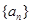 的通项公式;
的通项公式;
(Ⅱ)设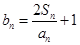 ,若数列
,若数列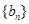 为等比数列,求
为等比数列,求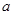 的值,并证明此时
的值,并证明此时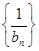 为“嘉文”数列.
为“嘉文”数列.
(I)∴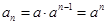 .
.
(II)由(I)知,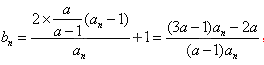 ,
,
若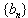 为等比数列,则有
为等比数列,则有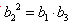 ,而
,而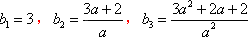 。
。
故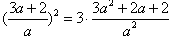 ,解得
,解得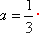 ,再将
,再将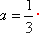 代入得:
代入得: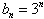 ,其为等比数列,所以
,其为等比数列,所以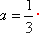 成立。由于①
成立。由于① 。
。
②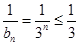 ,故存在
,故存在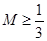 ;
;
所以符合①②,故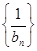 为“嘉文”数列。
为“嘉文”数列。
解析

练习册系列答案
相关题目
定义数列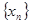 :
: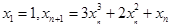 ;数列
;数列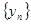 :
: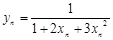 ;数列
;数列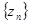 :
: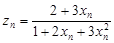 ;若
;若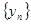 的前n项的积为
的前n项的积为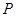 ,
,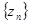 的前n项的和为
的前n项的和为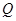 ,那么
,那么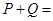 ( )
( )
A. | B.2 | C.3 | D.不确定 |
数列{an}的通项公式为an=(-1)n-1·(4n-3),则它的前100项之和S100等于( )
| A.200 | B.-200 | C.400 | D.-400 |
 中,前n项和为
中,前n项和为 ,且
,且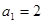 ,且
,且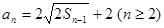 .
.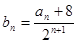 ,
,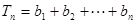 ,证明
,证明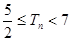 .
.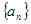 的前
的前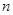 项和为
项和为 ,
,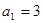 ,若数列
,若数列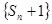 是公比为
是公比为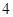 的等比数列.
的等比数列. 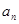 ;
;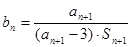 ,
,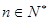 ,求数列
,求数列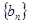 的前
的前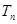 .
.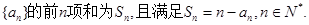
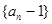 是等比数列;
是等比数列;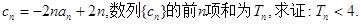
 满足
满足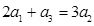 ,且
,且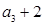 是
是 ,
, 的等差中项.
的等差中项. ,
, ,求使
,求使  成立的
成立的 的最小值.
的最小值.  x
x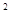 -
-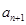 x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.
x+1=0(n∈N)有两根α和β,且满足6α-2αβ+6β=3.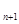 ;
;
 中,
中, ,其前
,其前 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,公比为
,公比为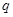 ,且
,且 ,
,  .
.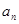 与
与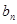 ;(Ⅱ)证明:
;(Ⅱ)证明: ≤
≤ .
.