题目内容
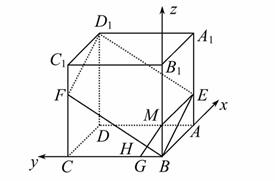
如图,已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,且AE=FC1=1.

(1)求证:E,B,F,D1四点共面;
(2)若点G在BC上,BG=![]() ,点M在BB1上,GM⊥BF,垂足为H,求证:
,点M在BB1上,GM⊥BF,垂足为H,求证:
EM⊥平面BCC1B1;
(3)用θ表示截面EBFD1和侧面BCC1B1所成的锐二面角的大小,求tanθ.
(1)建立如图所示的空间直角坐标系,
则![]() =(3,0,1),
=(3,0,1),![]() =(0,3,2),
=(0,3,2),![]() =(3,3,3),
=(3,3,3),
所以![]() =
=![]() +
+![]() ,
,
故![]() ,
,![]() ,
,![]() 共面.
共面.
又它们有公共点B,
所以E,B,F,D1四点共面.
(2)设M(0,0,z),则![]() =(0,-
=(0,-![]() ,z),
,z),
而![]() =(0,3,2),
=(0,3,2),
由题设得![]() ·
·![]()
![]() =-
=-![]() ×3+z·2=0,
×3+z·2=0,
得z=1.因为M(0,0,1),E(3,0,1),
有![]() =(3,0,0),
=(3,0,0),
又![]() =(0,0,3),
=(0,0,3),![]() =(0,3,0),
=(0,3,0),
所以![]() ·
·![]() =0,
=0,![]() ·
·![]() =0,
=0,
从而ME⊥BB1,ME⊥BC.
又BB1∩BC=B,
故ME⊥平面BCC1B1.
(3)设向量![]() =(x,y,3)且BP⊥截面EBFD1,
=(x,y,3)且BP⊥截面EBFD1,
于是![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() .
.
而![]() =(3,0,1),
=(3,0,1),![]() =(0,3,2),
=(0,3,2),
得![]() ·
·![]() =3x+3=0,
=3x+3=0,![]() ·
·![]() =3y+6=0,
=3y+6=0,
解得x=-1,y=-2,
所以![]() =(-1,-2,3).
=(-1,-2,3).
又![]() =(3,0,0)且BA⊥平面BCC1B1,
=(3,0,0)且BA⊥平面BCC1B1,
所以![]() 和
和![]() 的夹角等于θ或π-θ(θ为锐角).
的夹角等于θ或π-θ(θ为锐角).
于是cosθ=![]() =
=![]() .
.
故tanθ=![]() .
.

练习册系列答案
相关题目
 18、如图,已知ABCD是矩形,E是以CD为直径的半圆周上一点,且平面CDE⊥平面ABCD,求证:CE⊥平面ADE.
18、如图,已知ABCD是矩形,E是以CD为直径的半圆周上一点,且平面CDE⊥平面ABCD,求证:CE⊥平面ADE.
 (2012•汕头二模)如图,已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,
(2012•汕头二模)如图,已知ABCD-A1B1C1D1是底面边长为1的正四棱柱, 如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.
如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE. (2005•普陀区一模)如图,已知ABCD和A1B1C1D1都是正方形,且AB∥A1B1,AA1=BB1=CC1=DD1,若将图中已作出的线段的两个端点分别作为向量的始点和终点所形成的不相等的向量的全体构成集合M,则从集合M中任取两个向量恰为平行向量的概率是
(2005•普陀区一模)如图,已知ABCD和A1B1C1D1都是正方形,且AB∥A1B1,AA1=BB1=CC1=DD1,若将图中已作出的线段的两个端点分别作为向量的始点和终点所形成的不相等的向量的全体构成集合M,则从集合M中任取两个向量恰为平行向量的概率是