题目内容
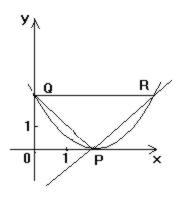
二次函数y=ax2+bx+c(a>0,b<0)的图象和x轴y轴都只有一个公共点,分别 记为P、Q,已知 │PQ│ =2
答案:4
解析:
提示:
解析:
|
解:∵抛物线与x轴只有一个交点P,
∴P点就是抛物线的顶点,其坐标为( ∵b+2ac=0
∴c=- ∴P点坐标为(c,0) ∵Q点是抛物线与y轴交点 ∴Q点坐标是(0,c)
∵ |PQ| =2
│PQ│ = ∴c=2,即P(2,0),Q(0,2)
联立得到二次函数解析式为
y= ∵y=x+m图象过P(2,0)点, ∴2+m=0,m=-2 ∴一次函数解析式为y=x-2
│PR│ = ∴│PQ│=│PR│,且 │RQ│=4,RQ∥x轴
∴S△PQR=
|
提示:
| 抛物线和x轴只有一个交点,这个交点是抛物线的顶点. |

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目