题目内容
为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
药物效果试验列联表
设从没服用药的动物中任取两只,未患病数为X;从服用药物的动物中任取两只,未患病数为Y,工作人员曾计算过P(X=0)=
P(Y=0).
(1)求出列联表中数据x,y,M,N的值;
(2)能够有多大的把握认为药物有效?
(3)现在从该100头动物中,采用随机抽样方法每次抽取1头,抽后返回,抽取5次,若每次抽取的结果是相互独立的,记被抽取的5头中为服了药还患病的数量为ξ.,求ξ的期望E(ξ)和方差D(ξ).
参考公式:x2=
(其中n=a+b+c+d)
药物效果试验列联表
| 患病 | 未患病 | 总计 | |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | x | y | 50 |
| 总计 | M | N | 100 |
| 38 |
| 9 |
(1)求出列联表中数据x,y,M,N的值;
(2)能够有多大的把握认为药物有效?
(3)现在从该100头动物中,采用随机抽样方法每次抽取1头,抽后返回,抽取5次,若每次抽取的结果是相互独立的,记被抽取的5头中为服了药还患病的数量为ξ.,求ξ的期望E(ξ)和方差D(ξ).
参考公式:x2=
| n(ad-bc)2 |
| (a+b)(b+c)(a+c)(b+d) |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 1.323 | 2.072 | 2.706 | 3.845 | 6.635 | 7.879 |
(1)∵用分层抽样的方法,从50只服用药的动物中抽查10个进行重点跟踪试验,其中患病的有2只,
∴
=
,
∴x=10,
∴y=50-10=40,
∴M=20+10=30,N=30+40=70,
即x=10,y=40,M=30,N=70;
(2)∵K2=
≈4.76<5.204
∴由参考数据知不能够以95%的把握认为药物有效;
(3)从该100头动物中,采用随机抽样方法每次抽取1头的概率为p=0.1,
∴ξ~B(100,0.1),
∴ξ的期望E(ξ)=100×0.1=10,方差D(ξ)=100×0.1×(1-0.1)=9.
∴
| 2 |
| 10 |
| x |
| 50 |
∴x=10,
∴y=50-10=40,
∴M=20+10=30,N=30+40=70,
即x=10,y=40,M=30,N=70;
(2)∵K2=
| 100×(800-300)2 |
| 30×70×50×50 |
∴由参考数据知不能够以95%的把握认为药物有效;
(3)从该100头动物中,采用随机抽样方法每次抽取1头的概率为p=0.1,
∴ξ~B(100,0.1),
∴ξ的期望E(ξ)=100×0.1=10,方差D(ξ)=100×0.1×(1-0.1)=9.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求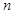 及天数如下表:
及天数如下表: