题目内容
小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数 及天数如下表:
及天数如下表:
试依据以频率估计概率的统计思想,解答下列问题:
(1)计算小王某天售出该现烤面包超过13个的概率;
(2)若在今后的连续5天中,售出该现烤面包超过13个的天数大于3天,则小王决定增加订购量.试求小王增加订购量的概率.
(3)若小王每天订购14个该现烤面包,求其一天出售该现烤面包所获利润的分布列和数学期望.
 及天数如下表:
及天数如下表:售出个数 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天数 | 3 | 3 | 3 | 6 | 9 | 6 |
(1)计算小王某天售出该现烤面包超过13个的概率;
(2)若在今后的连续5天中,售出该现烤面包超过13个的天数大于3天,则小王决定增加订购量.试求小王增加订购量的概率.
(3)若小王每天订购14个该现烤面包,求其一天出售该现烤面包所获利润的分布列和数学期望.
(1)0.5;(2)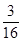 ;(3)分布列为
;(3)分布列为
数学期望为123.5元.
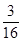 ;(3)分布列为
;(3)分布列为利润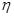 | 80 | 95 | 110 | 125 | 140 |
概率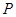 | 0.1 | 0.1 | 0.1 | 0.2 | 0.5 |
数学期望为123.5元.
试题分析:(1)由于小王某天售出该现烤面包超过13个的情况有三种:恰14个和恰15个,由题中表格易得:小王某天售出该现烤面包恰14个和恰15个的概率分别为
 ,再由小王某天售出该现烤面包恰14个和恰15个这两个事件是互斥的,所以小王某天售出该现烤面包超过13个的概率就等于上述两个概率之和为:0.3+0.2=0.5.
,再由小王某天售出该现烤面包恰14个和恰15个这两个事件是互斥的,所以小王某天售出该现烤面包超过13个的概率就等于上述两个概率之和为:0.3+0.2=0.5.(2)设在最近的5天中售出超过13个的天数为
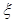 ,由于每天售出的个数要么超过13个,要么不超过13个只有这两种结果,且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变各为0.5,所以
,由于每天售出的个数要么超过13个,要么不超过13个只有这两种结果,且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变各为0.5,所以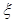 服从参数为5和0.5的二项分布,即
服从参数为5和0.5的二项分布,即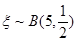 ,从而事件“小王增加订购量”的概率,即是
,从而事件“小王增加订购量”的概率,即是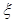 >3的概率,而
>3的概率,而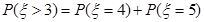 ,再由二项分布的概率公式
,再由二项分布的概率公式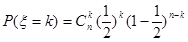 可算得事件“小王增加订购量”的概率;
可算得事件“小王增加订购量”的概率;(3)由于小王每天订购14个现烤面包,则可设其一天的利润为
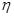 元,由已知求出
元,由已知求出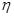 的所有可能取值,并结合题只所给条件可得到
的所有可能取值,并结合题只所给条件可得到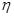 的每一个可能取值的概率,从而求得其分布列,在由数学期望公式:
的每一个可能取值的概率,从而求得其分布列,在由数学期望公式: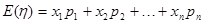 就可求得所获利润的数学期望.
就可求得所获利润的数学期望.试题解析:(1)记事件A=“小王某天售出超过13个现烤面包”, 1分
用频率估计概率可知:
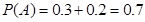 . 2分
. 2分所以小王某天售出超过13个现烤面包的概率为0.5. 3分
(2)设在最近的5天中售出超过13个的天数为
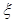 ,
, 则
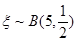 . ..5分
. ..5分记事件B=“小王增加订购量”,
则有
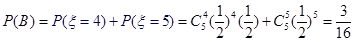 ,
,所以小王增加订购量的概率为
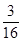 . 8分
. 8分(3)若小王每天订购14个现烤面包,设其一天的利润为
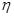 元,则
元,则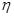 的所有可能取值为80,95,110,125,140. 9分
的所有可能取值为80,95,110,125,140. 9分其分布列为
利润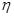 | 80 | 95 | 110 | 125 | 140 |
概率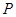 | 0.1 | 0.1 | 0.1 | 0.2 | 0.5 |
则
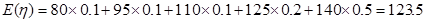
所以小王每天出售该现烤面包所获利润的数学期望为123.5元. ..13分

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 列联表:
列联表: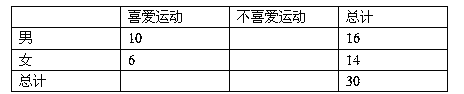
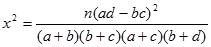 (其中
(其中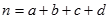 )
)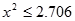
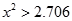
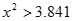
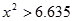
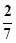 .
.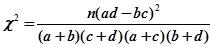 ,其中
,其中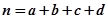 .
. ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联;
≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联;