题目内容
已知椭圆 的两个焦点分别为
的两个焦点分别为 ,且
,且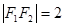 ,点
,点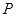 在椭圆上,且
在椭圆上,且 的周长为6.
的周长为6.
(I)求椭圆 的方程;
的方程;
(II)若点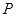 的坐标为
的坐标为 ,不过原点
,不过原点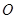 的直线与椭圆
的直线与椭圆 相交于
相交于 两点,设线段
两点,设线段 的中点为
的中点为 ,点
,点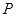 到直线的距离为
到直线的距离为 ,且
,且 三点共线.求
三点共线.求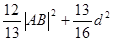 的最大值.
的最大值.
(Ⅰ)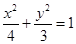 ;(Ⅱ)
;(Ⅱ)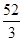 .
.
解析试题分析:(Ⅰ)根据题中条件确定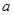 、
、 、
、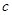 的值,进而确定椭圆
的值,进而确定椭圆 的方程;(Ⅱ)对直线
的方程;(Ⅱ)对直线 的斜率存在与否进行分类讨论,并在相应的情况下求出
的斜率存在与否进行分类讨论,并在相应的情况下求出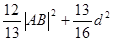 的最大值,并作出比较,尤其是在处理直线
的最大值,并作出比较,尤其是在处理直线 的斜率存在,一般将直线
的斜率存在,一般将直线 的方程设为
的方程设为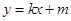 ,借助韦达定理,确定
,借助韦达定理,确定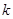 与
与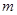 之间的关系,然后将
之间的关系,然后将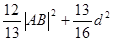 化为自变量为
化为自变量为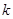 或
或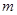 的函数,借助函数的最值来求取,但要注意相应自变量的取值范围.
的函数,借助函数的最值来求取,但要注意相应自变量的取值范围.
试题解析:解:(I)由已知得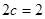 且
且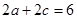 ,
,
解得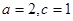 ,又
,又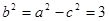 ,
,
所以椭圆 的方程为
的方程为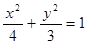 .
.
3分
(II)设 .
.
当直线与 轴垂直时,由椭圆的对称性可知,点
轴垂直时,由椭圆的对称性可知,点 在
在 轴上,且与
轴上,且与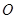 点不重合,
点不重合,
显然 三点不共线,不符合题设条件.
三点不共线,不符合题设条件.
故可设直线的方程为 .
.
由 消去
消去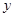 整理得
整理得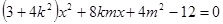 . ①
. ①
则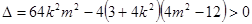 ,
,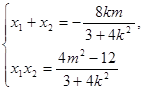 所以点
所以点 的坐标为
的坐标为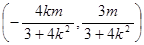 .
.
因为 三点共线,所以
三点共线,所以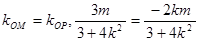 ,
,
因为 ,所以
,所以 ,
,
此时方程①为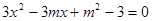 ,则
,则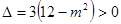 ,
,
所以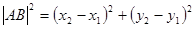
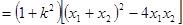
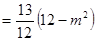 ,
,
又 ,
,
所以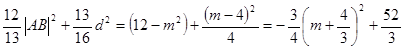 ,
,
故当 时,
时,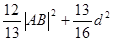 的最大值为
的最大值为 .[来源:学科网ZXXK]
.[来源:学科网ZXXK]
13分
考点:椭圆的方程、韦达定理、点到直线的距离

练习册系列答案
相关题目
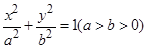 的长轴两端点分别为
的长轴两端点分别为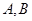 ,
, 是椭圆上的动点,以
是椭圆上的动点,以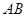 为一边在
为一边在 轴下方作矩形
轴下方作矩形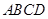 ,使
,使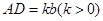 ,
, 交
交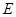 ,
, 交
交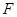 .
.
 ,且
,且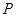 为椭圆上顶点时,
为椭圆上顶点时,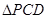 的面积为12,点
的面积为12,点 到直线
到直线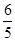 ,求椭圆的方程;
,求椭圆的方程; ,试证明:
,试证明: 成等比数列.
成等比数列.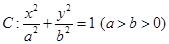 的右焦点为
的右焦点为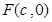 ,上顶点为B,离心率为
,上顶点为B,离心率为 ,圆
,圆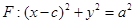 与
与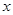 轴交于
轴交于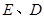 两点
两点 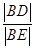 的值;
的值;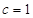 ,过点
,过点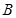 与圆
与圆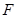 相切的直线
相切的直线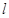 与
与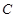 的另一交点为
的另一交点为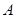 ,求
,求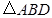 的面积
的面积 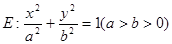 的离心率
的离心率 ,
,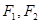 是其左右焦点,点
是其左右焦点,点 是直线
是直线 (其中
(其中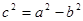 )上一点,且直线
)上一点,且直线 的倾斜角为
的倾斜角为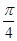 .
. 的方程;
的方程;  是椭圆
是椭圆 ,求
,求 (
(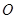 为坐标原点)面积的最小值.
为坐标原点)面积的最小值. 中,点
中,点 为动点,
为动点, 分别为椭圆
分别为椭圆 的左右焦点.已知△
的左右焦点.已知△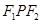 为等腰三角形.(1)求椭圆的离心率
为等腰三角形.(1)求椭圆的离心率 ;(2)设直线
;(2)设直线 与椭圆相交于
与椭圆相交于 两点,
两点, 是直线
是直线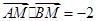 ,求点
,求点
 的焦点
的焦点 以及椭圆
以及椭圆 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆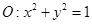 上.
上. 和椭圆
和椭圆 的标准方程;
的标准方程;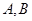 两不同点,交
两不同点,交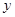 轴于点
轴于点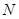 ,已知
,已知 ,求
,求 的值;
的值;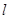 交椭圆
交椭圆 两不同点,
两不同点,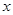 轴的射影分别为
轴的射影分别为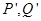 ,
, ,若点
,若点 满足
满足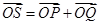 ,证明:点
,证明:点 年
年 月
月 日
日 时
时 分
分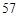 秒“嫦娥二号”探月卫星由长征三号丙运载火箭送入近地点高度约
秒“嫦娥二号”探月卫星由长征三号丙运载火箭送入近地点高度约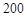 公里、远地点高度约
公里、远地点高度约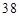 万公里的直接奔月椭圆(地球球心
万公里的直接奔月椭圆(地球球心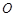 为一个焦点)轨道Ⅰ飞行。当卫星到达月球附近的特定位置时,实施近月制动及轨道调整,卫星变轨进入远月面
为一个焦点)轨道Ⅰ飞行。当卫星到达月球附近的特定位置时,实施近月制动及轨道调整,卫星变轨进入远月面 公里、近月面
公里、近月面 公里(月球球心
公里(月球球心 为一个焦点)的椭圆轨道Ⅱ绕月飞行,之后卫星再次择机变轨进入以
为一个焦点)的椭圆轨道Ⅱ绕月飞行,之后卫星再次择机变轨进入以 公里,月球半径约为
公里,月球半径约为 公里。
公里。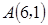 作直线与双曲线
作直线与双曲线 相交于两点
相交于两点 、
、 ,且
,且 为线段
为线段 的中点,求这条直线的方程.
的中点,求这条直线的方程.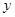 轴上,且过点
轴上,且过点 .
.
 相切的直线
相切的直线 交抛物线于不同的两点
交抛物线于不同的两点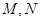 若抛物线上一点
若抛物线上一点 满足
满足 ,求
,求 的取值范围.
的取值范围.