题目内容
已知点A(4,-3),B(2,-1)和直线l:4x+3y-2=0,求一点P使|PA|=|PB|,且点P到l的距离等于2.
点P(1,-4)或P(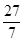 ,-
,-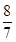 )为所求的点
)为所求的点
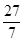 ,-
,-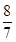 )为所求的点
)为所求的点为使|PA|=|PB|(如图),点P必在线段AB的垂直平分线上,又点P到直线l的距离为2,所以点P又在距离l为2且平行于l的直线上,求这两条直线的交点即得所求点P.设点P的坐标为P(a,b).
∵ A(4,-3),B(2,-1).∴ AB的中点M的坐标为(3,-2).又AB的斜率kAB=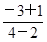 =-1.∴ AB的垂直平分线方程为y+2=x-3,即x-y-5=0.
=-1.∴ AB的垂直平分线方程为y+2=x-3,即x-y-5=0.
而P(a,b)在直线x-y-5=0上.∴ a-b-5=0①.
又已知点P到l的距离为2,∴ 点P必在与l平行且距离为2的直线上,设直线方程为4x+3y+m=0,由两条平行直线之间的距离公式,得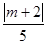 =2,
=2,
∴ m=8或-12.∴ 点P在直线4x+3y+8=0或4x+3y-12=0上.∴ 4a+3b+8=0或4a+3b-12=0 ②.由①②得a=1,b=-4或a=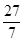 ,b=-
,b=-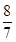 .
.
∴ 点P(1,-4)或P(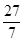 ,-
,-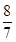 )为所求的点
)为所求的点

∵ A(4,-3),B(2,-1).∴ AB的中点M的坐标为(3,-2).又AB的斜率kAB=
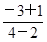 =-1.∴ AB的垂直平分线方程为y+2=x-3,即x-y-5=0.
=-1.∴ AB的垂直平分线方程为y+2=x-3,即x-y-5=0. 而P(a,b)在直线x-y-5=0上.∴ a-b-5=0①.
又已知点P到l的距离为2,∴ 点P必在与l平行且距离为2的直线上,设直线方程为4x+3y+m=0,由两条平行直线之间的距离公式,得
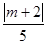 =2,
=2,∴ m=8或-12.∴ 点P在直线4x+3y+8=0或4x+3y-12=0上.∴ 4a+3b+8=0或4a+3b-12=0 ②.由①②得a=1,b=-4或a=
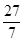 ,b=-
,b=-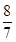 .
.∴ 点P(1,-4)或P(
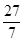 ,-
,-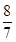 )为所求的点
)为所求的点
练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
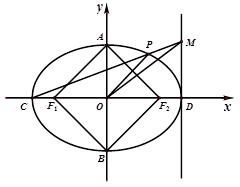
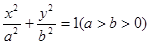 的左右焦点分别为
的左右焦点分别为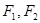 ,短轴两个端点为
,短轴两个端点为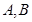 ,且四边形
,且四边形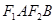 是边长为2的正方形.
是边长为2的正方形.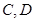 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点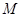 满足
满足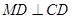 ,连接
,连接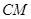 ,交椭圆于点
,交椭圆于点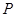 .证明:
.证明: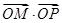 为定值;
为定值;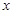 轴上是否存在异于点
轴上是否存在异于点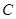 的定点
的定点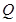 ,使得以
,使得以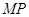 为直径的圆恒过直线
为直径的圆恒过直线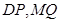 的交点,若存在,求出点
的交点,若存在,求出点