题目内容
过点A（-1，0）的直线l与抛物线y=x2只有一个公共点，则这样的直线有________条．
3
分析：考虑斜率存在与不存在，分别求出切线方程，即可得到结论．
解答：设过点A（-1，0）的直线l的方程为y=k（x+1），代入抛物线y=x2，化简可得x2-kx-k=0
∵过点A（-1，0）的直线l与抛物线y=x2只有一个公共点，
∴△=k2+4k=0
∴k=0或-4
切线方程为y=0或y=-4x-4
当斜率不存在时，x=-1满足题意
故答案为：3
点评：本题考查直线与抛物线的位置关系，考查分类讨论的数学思想，属于基础题．
分析：考虑斜率存在与不存在，分别求出切线方程，即可得到结论．
解答：设过点A（-1，0）的直线l的方程为y=k（x+1），代入抛物线y=x2，化简可得x2-kx-k=0
∵过点A（-1，0）的直线l与抛物线y=x2只有一个公共点，
∴△=k2+4k=0
∴k=0或-4
切线方程为y=0或y=-4x-4
当斜率不存在时，x=-1满足题意
故答案为：3
点评：本题考查直线与抛物线的位置关系，考查分类讨论的数学思想，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
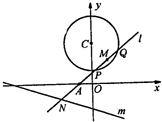已知过点A（-1，0）的动直线l与圆C：x2+（y-3）2=4相交于P，Q两点，M是PQ中点，l与直线m：x+3y+6=0相交于N．
已知过点A（-1，0）的动直线l与圆C：x2+（y-3）2=4相交于P、Q两点，M是PQ中点，l与直线m：x+3y+6=0相交于点N．