题目内容
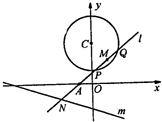已知过点A（-1，0）的动直线l与圆C：x2+（y-3）2=4相交于P，Q两点，M是PQ中点，l与直线m：x+3y+6=0相交于N．（1）求证：当l与m垂直时，l必过圆心C；
（2）当PQ=2
| 3 |
（3）探索
| AM |
| AN |
分析：（1）根据l与m垂直，则两条直线的斜率之积为-1，进而根据直线过点A（-1，0），我们可求出直线的方程，将圆的圆心坐标代入直线方程验证后，即可得到结论；
（2）根据半弦长、弦心距、圆半径构造直角三角形，满足勾股定理，结合PQ=2
，易得到弦心距，进而根据点到直线的距离公式，构造关于k的方程，解方程即可得到k值，进而得到直线l的方程；
（3）根据已知条件，我们可以求出两条直线的交点N的坐标（含参数k），然后根据向量数量积公式，即可求出
•
的值，进而得到结论．
（2）根据半弦长、弦心距、圆半径构造直角三角形，满足勾股定理，结合PQ=2
| 3 |
（3）根据已知条件，我们可以求出两条直线的交点N的坐标（含参数k），然后根据向量数量积公式，即可求出
| AM |
| AN |
解答：解：（1）∵l与m垂直，且km=-
，∴k1=3，
故直线l方程为y=3（x+1），即3x-y+3=0．∵圆心坐标（0，3）满足直线l方程，
∴当l与m垂直时，l必过圆心C．
（2）①当直线l与x轴垂直时，易知x=-1符合题意．
②当直线l与x轴不垂直时，设直线l的方程为y=k（x+1），即kx-y+k=0，
∵PQ=2
，∴CM=
=1，则由CM=
=1，得k=
，
∴直线l：4x-3y+4=0．
故直线l的方程为x=-1或4x-3y+4=0．
（3）∵CM⊥MN，∴
•
=(
+
)•
=
•
+
•
=
•
．
①当l与x轴垂直时，易得N(-1，-
)，则
=(0，-
)，又
=(1，3)，
∴
•
=
•
=-5．
②当l的斜率存在时，设直线l的方程为y=k（x+1），
则由
得N(
，
)，则
=(
，
)．
∴
•
=
•
=
+
=-5．
综上所述，a=18与直线l的斜率无关，且
•
=-5．
| 1 |
| 3 |
故直线l方程为y=3（x+1），即3x-y+3=0．∵圆心坐标（0，3）满足直线l方程，
∴当l与m垂直时，l必过圆心C．
（2）①当直线l与x轴垂直时，易知x=-1符合题意．
②当直线l与x轴不垂直时，设直线l的方程为y=k（x+1），即kx-y+k=0，
∵PQ=2
| 3 |
| 4-3 |
| |-k+3| | ||
|
| 4 |
| 3 |
∴直线l：4x-3y+4=0．
故直线l的方程为x=-1或4x-3y+4=0．
（3）∵CM⊥MN，∴
| AM |
| AN |
| AC |
| CM |
| AN |
| AC |
| AN |
| CM |
| AN |
| AC |
| AN |
①当l与x轴垂直时，易得N(-1，-
| 5 |
| 3 |
| AN |
| 5 |
| 3 |
| AC |
∴
| AM |
| AN |
| AC |
| AN |
②当l的斜率存在时，设直线l的方程为y=k（x+1），
则由
|
| -3k-6 |
| 1+3k |
| -5k |
| 1+3k |
| AN |
| -5 |
| 1+3k |
| -5k |
| 1+3k |
∴
| AM |
| AN |
| AC |
| AN |
| -5 |
| 1+3k |
| -15k |
| 1+3k |
综上所述，a=18与直线l的斜率无关，且
| AM |
| AN |
点评：本题考查的知识点是直线与圆相交的性质及向量在几何中的应用，其中在处理圆的弦长问题时，根据半弦长、弦心距、圆半径构造直角三角形，满足勾股定理，进行弦长、弦心距、圆半径的知二求一，是解答此类问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知过点A（-1，0）的动直线l与圆C：x2+（y-3）2=4相交于P、Q两点，M是PQ中点，l与直线m：x+3y+6=0相交于点N．
已知过点A（-1，0）的动直线l与圆C：x2+（y-3）2=4相交于P，Q两点，M是PQ的中点，l与直线m：x+3y+6=0相交于点N，则下面运算结果为定值的有（ ）
与圆C：
相交于P、Q两点，M是PQ的中点，
与直线m：
相交于N。
时，求直线
的方程；
是否与直线
的倾斜角有关，若无关，请求出其值；若有关，请说明理由。
已知过点A（-1，0）的动直线l与圆C：x2+（y-3）2=4相交于P，Q两点，M是PQ中点，l与直线m：x+3y+6=0相交于N．
时，求直线l的方程；
是否与直线l的倾斜角有关？若无关，请求出其值；若有关，请说明理由．