题目内容
若圆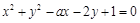 关于直线x – y – 1 = 0对称的圆的方程是
关于直线x – y – 1 = 0对称的圆的方程是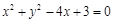 ,则a的值等于( )
,则a的值等于( )
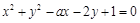 关于直线x – y – 1 = 0对称的圆的方程是
关于直线x – y – 1 = 0对称的圆的方程是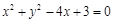 ,则a的值等于( )
,则a的值等于( )| A.0 | B.2 | C.– 2 | D.± 2 |
C
答案为B
由题意可得两圆的圆心的连线和对称轴垂直,斜率之积等于-1,求出a的值.
解答:解:由于圆x2+y2-ax-2y+1=0的圆心M( ,1),圆的方程是x2+y2-4x+3=0的圆心N(2,0),
,1),圆的方程是x2+y2-4x+3=0的圆心N(2,0),
由于圆x2+y2-ax-2y+1=0关于直线x-y-1=0对称的圆的方程是x2+y2-4x+3=0,故有
 ×1=-1,解得 a=2,
×1=-1,解得 a=2,
故答案为B.
由题意可得两圆的圆心的连线和对称轴垂直,斜率之积等于-1,求出a的值.
解答:解:由于圆x2+y2-ax-2y+1=0的圆心M(
 ,1),圆的方程是x2+y2-4x+3=0的圆心N(2,0),
,1),圆的方程是x2+y2-4x+3=0的圆心N(2,0),由于圆x2+y2-ax-2y+1=0关于直线x-y-1=0对称的圆的方程是x2+y2-4x+3=0,故有
 ×1=-1,解得 a=2,
×1=-1,解得 a=2,故答案为B.

练习册系列答案
相关题目
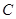 的方程为
的方程为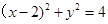 ,圆
,圆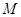 的方程为
的方程为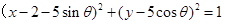
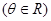 ,过圆
,过圆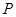 作圆
作圆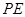 、
、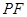 ,切点分别为
,切点分别为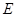 、
、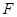 ,则
,则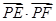 的最小值是( )
的最小值是( )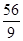
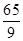
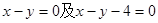 都相切,圆心在直线
都相切,圆心在直线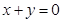 上,则圆C的方程为()
上,则圆C的方程为() 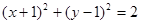
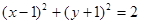
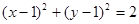
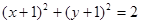
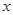 轴的正半轴上,且经过点
轴的正半轴上,且经过点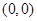 ,直线
,直线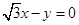 被该圆截得的弦长为
被该圆截得的弦长为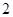 ,则该圆的方程是( )
,则该圆的方程是( )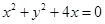
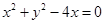
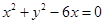
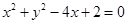
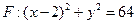 (F为圆心
(F为圆心 )上一点,线段AB的垂直平分线交BF于P.
)上一点,线段AB的垂直平分线交BF于P. 

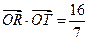 (O为原点).若存在,求直线l的方程;若不存在,请说明理由.
(O为原点).若存在,求直线l的方程;若不存在,请说明理由.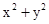 -2x-4y=0的圆心到直线x-y+a=0的距离为
-2x-4y=0的圆心到直线x-y+a=0的距离为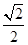 ,则a的值为
,则a的值为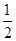 或
或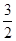
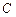 :
: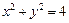 .
.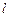 过点
过点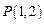 ,且与圆
,且与圆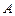 、
、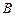 两点,若
两点,若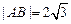 ,求直线
,求直线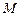 作平行于
作平行于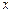 轴的直线
轴的直线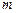 ,设
,设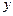 轴的交点为
轴的交点为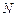 ,若向量
,若向量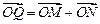 ,求动点
,求动点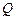 的轨迹方程.
的轨迹方程.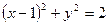 的位置关系是( )
的位置关系是( )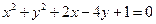 关于直线
关于直线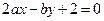 (a>0b>0)对称,则
(a>0b>0)对称,则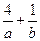 的最小值是( )
的最小值是( )