题目内容
已知一个圆的圆心在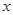 轴的正半轴上,且经过点
轴的正半轴上,且经过点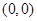 ,直线
,直线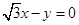 被该圆截得的弦长为
被该圆截得的弦长为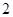 ,则该圆的方程是( )
,则该圆的方程是( )
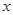 轴的正半轴上,且经过点
轴的正半轴上,且经过点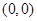 ,直线
,直线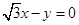 被该圆截得的弦长为
被该圆截得的弦长为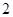 ,则该圆的方程是( )
,则该圆的方程是( )A.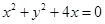 | B.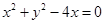 |
C.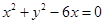 | D.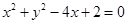 |
B
分析:根据一个圆的圆心在x轴的正半轴上,设出圆心坐标为(a,0),且a大于0,半径为r,表示出圆的标准方程,由圆经过(0,0),把(0,0)代入所设的圆的方程,得到a=r,可得到圆心坐标为(r,0),然后利用点到直线的距离公式表示出圆心到已知直线的距离d,由已知弦长的一半,圆的半径r以及d,利用勾股定理列出关于r的方程,求出方程的解可得到r的值,确定出圆心坐标和半径,进而确定出圆的标准方程.
解答:解:由题意设圆心坐标为(a,0)(a>0),圆的半径为r,
∴圆的方程为(x-a)2+y2=r2(r>0),
又圆经过(0,0),
∴a2=r2,即a=r,
∴圆心坐标为(r,0),
∴圆心到直线
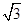 x-y=0的距离d=
x-y=0的距离d=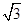
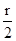 ,
,
又弦长为2,即弦长的一半为1,
∴r2=d2+12,即r2=
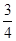 r2+1,
r2+1,
解得:r=2,
∴圆心坐标为(2,0),半径r=2,
则圆的标准方程为:(x-2)2+y2=4,即x2+y2-4x=0.
故选B
解答:解:由题意设圆心坐标为(a,0)(a>0),圆的半径为r,
∴圆的方程为(x-a)2+y2=r2(r>0),
又圆经过(0,0),
∴a2=r2,即a=r,
∴圆心坐标为(r,0),
∴圆心到直线
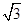 x-y=0的距离d=
x-y=0的距离d=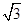
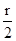 ,
,又弦长为2,即弦长的一半为1,
∴r2=d2+12,即r2=
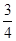 r2+1,
r2+1,解得:r=2,
∴圆心坐标为(2,0),半径r=2,
则圆的标准方程为:(x-2)2+y2=4,即x2+y2-4x=0.
故选B

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
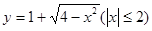 与直线
与直线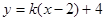 有两个交点时,实数k的取值范围是 ( )
有两个交点时,实数k的取值范围是 ( )
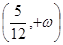
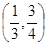

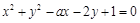 关于直线x – y – 1 = 0对称的圆的方程是
关于直线x – y – 1 = 0对称的圆的方程是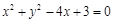 ,则a的值等于( )
,则a的值等于( )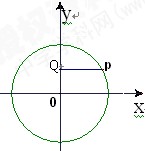
 过圆O上任P一点作y轴的垂线,垂足为Q,求线段PQ的中点M的轨迹方程。(12分)
过圆O上任P一点作y轴的垂线,垂足为Q,求线段PQ的中点M的轨迹方程。(12分)
 .
.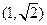 的直线l将圆C:(x-2)2+y2=4分成两段弧,当劣弧所对的圆心角最小时,直线l的斜率k= ▲
的直线l将圆C:(x-2)2+y2=4分成两段弧,当劣弧所对的圆心角最小时,直线l的斜率k= ▲ 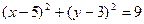 上的点,则M到直线
上的点,则M到直线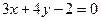 的最长距离是 .
的最长距离是 .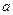 x-y+3=0与圆
x-y+3=0与圆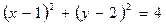 相交于A,B两点,且弦AB的长为
相交于A,B两点,且弦AB的长为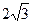 ,则
,则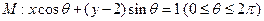 ,对于下列四个命题:
,对于下列四个命题: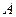 .存在一个圆与所有直线相交
.存在一个圆与所有直线相交 
 .存在一个圆与所有直线不相交
.存在一个圆与所有直线不相交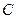 .存在一个圆与所有直线相切
.存在一个圆与所有直线相切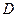 .
.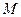 中的直线所能围成的正三角形面积都相等
中的直线所能围成的正三角形面积都相等