题目内容
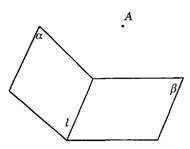
根据叙述作图,指出二面角α-l-β的平面角,并证明.
(1)已知α∩β=l,A∈l(下图).在α内作PA⊥l于A,在β内作QA⊥l于A.

(2)已知α∩β=l,A∈α,![]() (下图).作AP⊥β于P,在α内作AQ⊥l于Q,连结PQ.
(下图).作AP⊥β于P,在α内作AQ⊥l于Q,连结PQ.

(3)已知α∩β=l,![]() ,
,![]() (下图).作AP⊥α于P,AQ⊥β于Q,l∩平面PAQ=H,连结PH、QH.
(下图).作AP⊥α于P,AQ⊥β于Q,l∩平面PAQ=H,连结PH、QH.

答案:
解析:
解析:
|
解析:(1)PA (2)∵AP⊥β,∴PQ为AQ在平面β内的射影,∵AQ⊥l,根据三垂线定理,有PQ⊥l,∴∠AQP为二面角的平面角. (3)∵AP⊥α,∴AP⊥l,∵AQ⊥β,∴AQ⊥l,∴l⊥平面PAQ,∵PH·QH |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
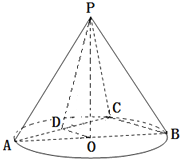 如图,在体积为
如图,在体积为