Question

作出下列函数的图象，并回答问题．（不用列表，不用叙述作图过程，但要标明必要的点或线）（1）f(x)=

x

x+1

（2）g（x）=|2^-x-1|
①写出函数f（x）的单调区间及其单调性

 

．
②若方程g（x）=a有两个不同实数解，则a的取值范围是

 

．

Answer 1

分析：本题考查的是函数的图象及其应用问题．在解答时应先根据对应的基本初等函数通过变换获得函数的图象，然后有函数的图象即可直观的读出函数的单调性，以及当方程g（x）=a有两个不同实数解时a的取值范围．

解答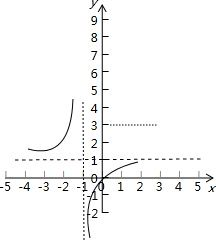：解：由题意可知函数f(x)=

x

x+1

的图象为：
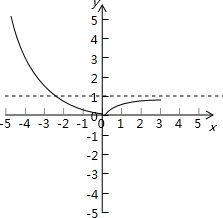
函数g(x)=|2-x-1| =

2-x-1，x≤0  -2-x+1，x＞0

的图象为：

由图象知函数f（x）的单调增区间为：（-∞，-1）和（-1，+∞）．
若方程g（x）=a有两个不同实数解，则a的取值范围是：0＜a＜1．
故答案为：（-∞，-1）和（-1，+∞）、0＜a＜1．

点评：本题考查的是函数的图象及其应用问题．在解答的过程当中充分体现了函数图象的变换以及数形结合的思想．值得同学们体会反思．