题目内容
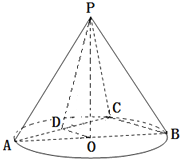 如图,在体积为
如图,在体积为
| ||
| 3 |
 |
| AB |
(1)指出二面角D-PO-A的平面角,并求出它的大小;
(2)求异面直线PD与BC所成的角的正切值.
分析:(1)由题意可得二面角D-PO-A的平面角为∠AOD,解三角形可得;
(2)可得∠PDO为异面直线PD,BC所成的角,在Rt△PDO中,易得答案.
(2)可得∠PDO为异面直线PD,BC所成的角,在Rt△PDO中,易得答案.
解答:解:(1)∵圆锥PO中PO⊥平面AOD,
∴AO⊥PO,DO⊥PO
∴二面角D-PO-A的平面角为∠AOD,
由已知易得△OD为等腰直角三角形,
∴∠AOD=∠A=45°;
(2)在△ABC中OD∥BC,
故∠PDO为异面直线PD,BC所成的角,
∵AB=2,∴BC=
,∴DO=
,
由体积公式可得
π×12×PO=
π,解得PO=
,
∴在Rt△PDO中,tan∠PDO=
=2.
∴所求的正切值为2.
∴AO⊥PO,DO⊥PO
∴二面角D-PO-A的平面角为∠AOD,
由已知易得△OD为等腰直角三角形,
∴∠AOD=∠A=45°;
(2)在△ABC中OD∥BC,
故∠PDO为异面直线PD,BC所成的角,
∵AB=2,∴BC=
| 2 |
| ||
| 2 |
由体积公式可得
| 1 |
| 3 |
| ||
| 3 |
| 2 |
∴在Rt△PDO中,tan∠PDO=
| PO |
| DO |
∴所求的正切值为2.
点评:本题考查异面直线所成的角,涉及二面角的求解,属中档题.

练习册系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,点M为侧棱AA1上一动点,已知△BCM面积的最大值是2
如图,在正三棱柱ABC-A1B1C1中,点M为侧棱AA1上一动点,已知△BCM面积的最大值是2 如图,在三棱柱ABC-A1B1C1中,△ABC为等边三角形,侧棱AA1⊥平面ABC,
如图,在三棱柱ABC-A1B1C1中,△ABC为等边三角形,侧棱AA1⊥平面ABC, (2010•广州模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB,点E是PD的中点.
(2010•广州模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB,点E是PD的中点. (2013•绍兴一模)如图,在梯形ABCD中,AB∥CD,AB⊥AD,AD=4,点P在平面ABCD上的射影中点O,且
(2013•绍兴一模)如图,在梯形ABCD中,AB∥CD,AB⊥AD,AD=4,点P在平面ABCD上的射影中点O,且