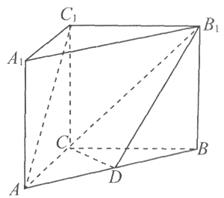
题目内容
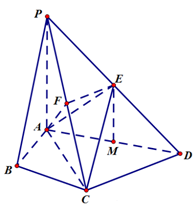
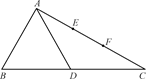
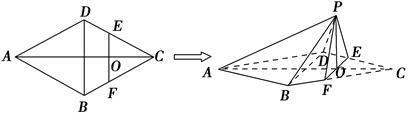
在四棱锥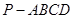 中,
中,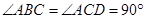 ,
, ,
, ,
, 为
为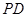 的中点,
的中点, 为
为 的中点,
的中点,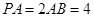 .
.
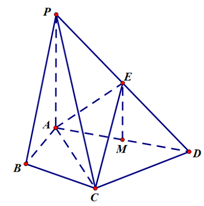
(1)求证: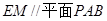 ;
;
(2)求证: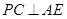 ;
;
(3)求三棱锥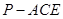 的体积
的体积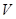 .
.
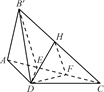
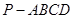 中,
中,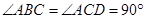 ,
, ,
, ,
, 为
为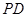 的中点,
的中点, 为
为 的中点,
的中点,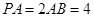 .
.
(1)求证:
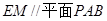 ;
;(2)求证:
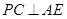 ;
;(3)求三棱锥
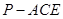 的体积
的体积 .
.(1)证明过程详见试题解析;(2)证明过程详见试题解析;(3)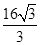 .
.
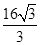 .
.试题分析:(1)由
 为
为 的中点,
的中点, 为
为 的中点,可得
的中点,可得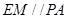 ,
,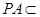 平面
平面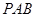 ,那么由线面平行的判定可以得到
,那么由线面平行的判定可以得到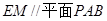 ;(2)取
;(2)取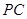 的中点
的中点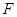 ,连结
,连结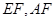 ,由于
,由于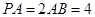 ,
,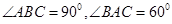 ,所以
,所以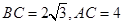 ,那么
,那么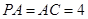 ,故
,故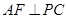 ,又
,又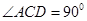 ,
,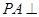 平面
平面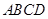 ,有
,有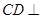 平面
平面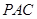 ,得到
,得到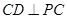 ,即
,即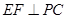 ,从而得到
,从而得到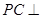 平面
平面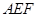 ,从而得到
,从而得到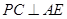 ; (3)要求三棱锥
; (3)要求三棱锥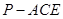 的体积
的体积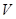 ,由(2)有
,由(2)有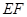 为三棱锥
为三棱锥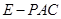 的高,利用体积公式求出即可.
的高,利用体积公式求出即可.试题解析:(1)因为
 为
为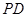 的中点,
的中点, 为
为 的中点,则在
的中点,则在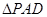 的中,
的中,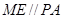
又
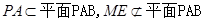
则
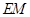 ∥平面
∥平面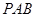 .
.(2)证明:取
 中点
中点 ,连接
,连接 .
.
在
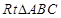 中,
中,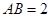 ,
,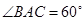 ,
,则
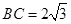 ,
,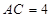 .
. 而
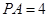 ,则在等腰三角形
,则在等腰三角形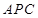 中
中 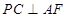 . ①
. ①又在
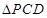 中,
中,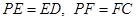 ,
, 则
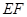 ∥
∥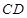
因为
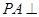 平面
平面 ,
,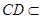 平面
平面 ,则
,则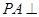
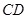 ,
,又
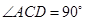 ,即
,即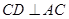 ,则
,则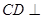 平面
平面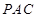 ,所以
,所以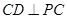
因此
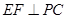 . ②
. ②又
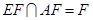 ,由①②知
,由①②知 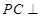 平面
平面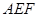 .
. 故
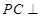
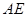
(3)由(1)(2)知
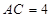 ,
, 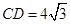 ,
,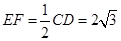
因为
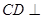 平面
平面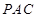 ,
, 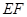 ∥
∥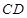 ,则
,则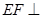 平面
平面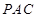
因此
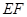 为三棱锥
为三棱锥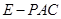 的高
的高 而
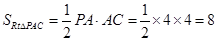
故
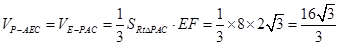

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 中,
中, ,
,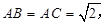
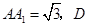 是
是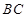 中点,
中点,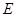 是
是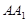 中点.
中点.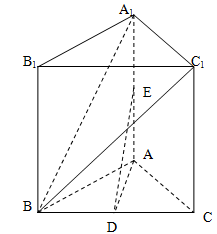
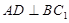 ;
;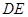 ∥面
∥面 .
.
 ,求此时线段PO的长.
,求此时线段PO的长.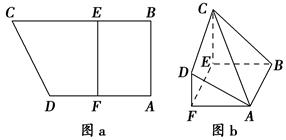
 =2,点G为AC的中点.
=2,点G为AC的中点.
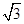 的正三角形,侧棱垂直于底面,且该三棱柱的外接球的体积为
的正三角形,侧棱垂直于底面,且该三棱柱的外接球的体积为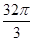 ,则该三棱柱的体积为________.
,则该三棱柱的体积为________.