题目内容
(2012•兰州模拟)曲线y=
x2-x-2在点(0,-2)处的切线与直线x=0和y=x+2所围成的区域内(包括边界)有一动点P(x,y),若z=2x-y,则z的取值范围是( )
| 1 |
| 2 |
分析:先求切线方程,再确定平面区域,明确目标函数的几何意义,即可确定z的取值范围.
解答:解:求导数可得:y′=x-1,令x=0,则y′=-1,∴曲线y=
x2-x-2在点(0,-2)处的切线方程为y=-x-2
∴切线y=-x-2与直线x=0和y=x+2所围成的区域如图:
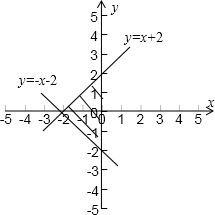
目标函数z=2x-y的几何意义是直线y=2x-z的纵截距的相反数
当过点(0,-2)时,z取得最大值2;当过点(-2,0)时,z取得最小值-4
∴z的取值范围是[-4,2]
故选D.
| 1 |
| 2 |
∴切线y=-x-2与直线x=0和y=x+2所围成的区域如图:

目标函数z=2x-y的几何意义是直线y=2x-z的纵截距的相反数
当过点(0,-2)时,z取得最大值2;当过点(-2,0)时,z取得最小值-4
∴z的取值范围是[-4,2]
故选D.
点评:本题考查导数的几何意义,考查线性规划知识,确定平面区域是关键.

练习册系列答案
相关题目