题目内容
【题目】已知,函数
其中
（1）讨论函数
的单调性；
（2）若函数有两个零点，
(i)求
的取值范围；
(ii)设的两个零点分别为x1,x2，证明：x1x2>e2．
【答案】（1）见解析（2）(i)
；(ii)见解析
【解析】
（1）求导后，分别在
和
两种情况下讨论导函数的符号，从而得到单调区间；（2）(i)将问题转化为
与函数
的图象在
上有两个不同交点，通过求解相切时的临界值，得到
的取值范围；(ii)将问题转化为证明
成立，通过构造函数
，证得
，从而证得结论.
（1）函数的定义域为，
①当时，
，
在单调递增；
②当时，由
得
，
则当
时，
，在
单调递增；
当
时，
，在
单调递减
（2）(i)函数有两个零点即方程
在有两个不同根
转化为函数与函数的图象在上有两个不同交点
如图：
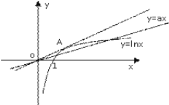
可见，若令过原点且切于函数图象的直线斜率为
，只需
设切点
，所以
又
，所以
，解得
于是
，所以
(ii)原不等式
不妨设
，
令
，则
，于是
设函数，
求导得：
故函数
是
上的增函数 
即不等式
成立，故所证不等式
成立
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+
)(A>0，ω>0，||<
)在某一个周期内的图象时，列表并填入了部分数据，如表：
ωx+ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+ | 0 | 5 | -5 | 0 |
（1）请将上表数据补充完整，并求出函数f(x)的解析式；
（2）将y=f(x)的图象向左平移
个单位，得到函数y=g(x)的图象.若关于x的方程g(x)-m=0在区间[0，]上有两个不同的解，求实数m的取值范围.
