题目内容
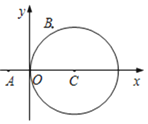
【题目】如图,在平面直角坐标系xOy中,已知圆C:x2+y2-4x=0及点A(-1,0),B(1,2)
(1)若直线l平行于AB,与圆C相交于M,N两点,MN=AB,求直线l的方程;
(2)若圆C上存在两个点P,使得PA2+PB2=a(a>4),求a的取值范围.
【答案】(1)x-y=0或x-y-4=0;(2)(22-8![]() ,22+8
,22+8![]() )
)
【解析】
(1)由题得直线AB方程为x-y+1=0, 设直线l的方程为x-y+m=0,由r2=(![]() )2+(
)2+(![]() )2,解得m=0或-4,即得直线l的方程为x-y=0或x-y-4=0;(2)设P(x,y),由题得x2+(y-1)2=
)2,解得m=0或-4,即得直线l的方程为x-y=0或x-y-4=0;(2)设P(x,y),由题得x2+(y-1)2=![]() -2,即得P的轨迹是以(0,1)为圆心,
-2,即得P的轨迹是以(0,1)为圆心,![]() 为半径的圆,由两圆相交可得
为半径的圆,由两圆相交可得![]() -2<
-2<![]() <
<![]() +2,解不等式即得a的取值范围.
+2,解不等式即得a的取值范围.
解:(1)根据题意,圆C的标准方程为(x-2)2+y2=4,
所以圆心C(2,0),半径为2.
因为l∥AB,A(-1,0),B(1,2),直线AB的方程为x-y+1=0,且|AB|=![]() =2
=2![]() ,
,
设直线l的方程为x-y+m=0,
又由MN=AB=2![]() ,圆心C到直线l的距离d=
,圆心C到直线l的距离d=![]()
则有r2=(![]() )2+(
)2+(![]() )2,即(
)2,即(![]() )2=2,解可得m=0或-4,
)2=2,解可得m=0或-4,
故直线l的方程为x-y=0或x-y-4=0;
(2)根据题意,设P(x,y),
若PA2+PB2=a,则PA2+PB2=(x+1)2+(y-0)2+(x-1)2+(y-2)2=a,
变形可得:x2+y2-2y+3=![]() ,即x2+(y-1)2=
,即x2+(y-1)2=![]() -2,
-2,
则P的轨迹是以(0,1)为圆心,![]() 为半径的圆;
为半径的圆;
若圆C上存在两个点P,使得PA2+PB2=a,则圆C与圆x2+(y-1)2=4相交,
两圆的圆心距d′=![]() =
=![]() ,
,
则有![]() -2<
-2<![]() <
<![]() +2,
+2,
解可得:22-8![]() <a<22+8
<a<22+8![]() ,
,
故a的取值范围为(22-8![]() ,22+8
,22+8![]() ).
).

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:

(1)根据箱产量的频率分布直方图填写下面![]() 列联表,从等高条形图中判断箱产量是否与新、旧网箱养殖方法有关;
列联表,从等高条形图中判断箱产量是否与新、旧网箱养殖方法有关;
(2)根据列联表判断是否有99%的把握认为箱产量与养殖方法有关?
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
参考公式:
(1)给定临界值表
P(K | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)![]() 其中
其中![]() 为样本容量.
为样本容量.
【题目】为了了解某省各景点在大众中的熟知度,随机对15~65岁的人群抽样了![]() 人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表
人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表
组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的频率 |
第1组 | [15,25) |
| 0.5 |
第2组 | [25,35) | 18 |
|
第3组 | [35,45) |
| 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 |
|

(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.


